Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas - Ex. 32

Considerando que a viga prismática AB tem uma seção transversal retangular, mostre que para a carregamento indicado o valor máximo da densidade de energia de deformação na viga é

M m a z = 45 8 U V

Em que U é a energia de deformação da viga e V é o seu volume.

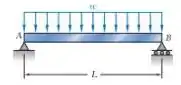
Passo 1

Calculando o momento temos:

+ ↺ M B = 0 :   - R A L + w L L 2 = 0     R A = 1 2 w L

M = R A x - 1 2 w L 2 = 1 2 w L x - x 2

Passo 2

A energia é dada por:

U = ∫ 0 L M 2 E I d x = w 2 8 E I ∫ 0 L L 2 x 2 - 2 L x 3 + x 4 d x = w 2 8 E I L 2 x 3 3 - 2 L x 4 4 + x 5 5 | 0 = w 2 L 5 8 E I 1 3 - 1 2 + 1 5 L

= w 2 L 5 240 E I

Passo 3

Temos o seguinte momento:

M m a x = 1 2 w L ∙ L 2 - L 2 2 = 1 8 w L 2

E a tensão é definida por:

σ m a x = M m a x C I = w L 2 c 8 I

u m a x = σ m a x 2 2 E = w 2 L 4 c 2 128 E I 2

U u m a x = 8 L I 15 c 2 = 8 L 1 12 b d 3 15 d 2 2

= 8 45 L b d = 8 45 V

u m a x = 45 8 U V

Resposta

45 8 U V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O membro cilíndrico A B , vazado e de paredes finas, tem uma seção transversal não-circular e espessura não uniforme. Usando a expressão τ dada na Eq. (3.53), da Sec. 3.13, e a expressão para densidad
Cada membro da treliça mostrada é feito de aço e tem uma seção transversal de área igual a 3230m m 2 . Usando-se E = 200G P a , determinar a deflexão vertical do ponto B , provocada pela carga de 90k
Cada um dos membros da treliça mostrada tem seção transversal uniforme de área A . Usando-se o método do trabalho e energia, determinar a deflexão vertical do ponto de aplicação da carga P .
Cada um dos membros da treliça mostrada é feita de aço e tem seção transversal de área igual a 400m m 2 . Usando-se E = 200G P a , determinar a deflexão no ponto D , provocada pela carga de 16N .
Usando o método do trabalho e energia, resolver o Prob. 3.34.