Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas - Ex. 33
Na montagem mostrada, os torques são aplicados nos discos A e B, respectivamente. Sabendo que ambos os eixos são maciços e feitos de alumínio ( determine a energia de deformação total acumulado pela montagem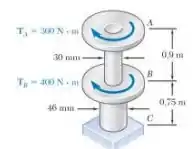
Passo 1
Na seção AB temos considerar que;;
Passo 2
A energia é dada por:
Na seção BC:
Total:
Resposta
Exercícios de Livros Relacionados
A barra de aço B C , de diâmetro 20m m , é presa à alavanca A B e ao apoio fixo C . A alavanca uniforme de aço tem 10m m de espessura e 30m m de largura. Usando o método do trabalho e energia, determi
Uma barra de aço de 15m m de diâmetro foi dobrada como mostrado. Usando o método do trabalho e energia, determinar a deflexão na extremidade C , devida à força P de 200N . Usar E = 200G P a e G = 77G
A barra de aço B C , de diâmetro 20m m , é presa à alavanca A B e ao apoio fixo C . A alavanca uniforme de aço tem 10m m de espessura e 30m m de largura. Usando o método do trabalho e energia, determi
Torques T de mesma intensidade são aplicados aos eixos de aço A B e C D . Usando o método do trabalho e energia, determinar o comprimento L da porção vazada do eixo C D , para que o ângulo de torção e
Dois eixos maciços de aço são conectados pelas engrenagens mostradas. Usando o método do trabalho e energia, determinar o ângulo de rotação da extremidade D , quando T = 820N × m . Usar G = 77G P a .