Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 115

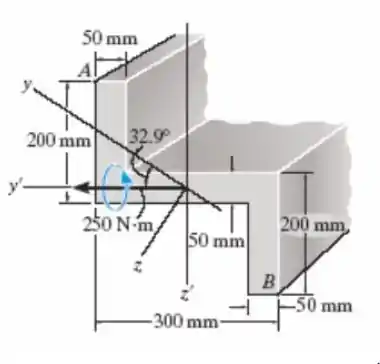
Usando as técnicas descritas no Apêndice A, Exemplo A.5 ou A.6, a seção em Z tem momentos principais de inércia Iy= 0,060(10-3)m4 e Iz= 0,471(10-3)m4, calculados em torno dos eixos principais de inércia y e z, respectivamente. Se a seção for submetida a um momento interno

M = 250 N · m direcionado na horizontal, como mostra a figura, determine a tensão produzida no ponto A, através da equação σ = [-(MzIy+MyIyz)y +(MyIz+MzIyz)z]/(IyIz-Iyz²).

Passo 1

Faaaala, meu povo bonito!! Tudo bem com vocês?? A questão de hoje tem essa cara meio estranha e formal, mas ele enrolou só pra dizer que os momentos de inércia, nos eixos y e z, são aqueles dados, e um momento M foi aplicado formando um ângulo de 32,9º em relação ao y com a horizontal. Depois desse monte de número, vamos determinar a tensão no ponto A. E aí, preparados?? Bora lá

Passo 2

O pontapé da nossa questão é redesenhar (sim, isso ajuda muito)!!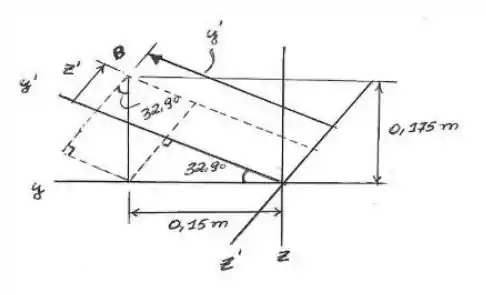

Agora que sabemos a cara do nosso sisteminha, vamos calcular os momentos de inércia para os dois eixos e o comum. Pelos nossos rabiscos, o y = 0,15 m, z = -0,175 m, Mz = 0, My = 250 N.m

Passo 3

I y   =   0,3   x   0,05 ³ 12 + 2 0,05   x   0,15 3 12 + 0,05 x 0,15 x 0,1 2 = 0,18125   x 10 - 3 m 4

I z   =   0,05   x   0,3 ³ 12 + 2 0,15   x   0,05 3 12 + 0,05 x 0,15 x 0,125 2 = 0,350   x 10 - 3 m 4

I y z   =   ( 0,15 ) ( 0,05 ) ( 0,125 ) ( - 0,1 ) + ( 0,15 ) ( 0,05 ) ( - 0,125 ) ( 0,1 )   =   - 0,1875   x   10 - 3   m 4

Agora que já temos os momentos necessários, vamos jogar lá na fórmula:

σ   =   - ( I y M z + M y I z y ) ( I y I z - I z y 2 )     y   +   I z M y + M z I z y ( I y I z - I z y 2 )     z   =   293 k P a

Resposta

σ   =   293 k P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A porção curva da barra mostrada tem um raio interno de 7,6 mm. A linha de ação da força de 270 N está localizada a uma distância a do plano que contém o centro de curvatura da barra. Determinar a mai
Para a barra curva e o carregamento mostrado, determinar o percentual de erro introduzido no cálculo da tensão máxima, assumindo-se que a barra é reta. Considerar o caso quando: r = 5m m r = 25m m r =
Sabendo-se que a tensão admissível de compressão é 80M P a , determinar a maior distância a permissível da linha de ação da força de 270N , ao plano que contém o centro de curvatura da barra.
A porção curva da barra mostrada tem um raio interno de 7,6 mm. A linha de ação da força de 270 N está localizada a uma distância a do plano que contém o centro de curvatura da barra. Determinar a mai
A barra prismática curva tem uma seção transversal de 5 × 7,5m m e um raio interno de r 1 = 15m m . Para o carregamento mostradado, determinar as maiores tensões de tração e compressão