Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 176

A barra prismática curva tem uma seção transversal de 5 × 7,5   m m e um raio interno de r 1 = 15   m m . Para o carregamento mostradado, determinar as maiores tensões de tração e compressão

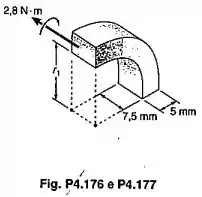
Passo 1

A questão já nos dá as dimensões da seção transversal, h = 5   m m b = 7,5   m m , e o raio interno r 1 = 15   m m . Com isso dá pra calcular o raio externo:

r 2 = 20   m m

E também já podemos calcular a área da seção transversal:

A = h b = 5   m m ⋅ 7,5   m m = 37,5   m m 2

Passo 2

Já r - é referente ao centroide. Como é um retângulo, o centroide se encontra no meio da seção. Logo:

r - = r 1 + h 2 = 15 + 5 2 = 17,5   m m

Como a seção é quadrada, o raio da linha neutra pode ser calculado:

R = h ln ⁡ r 2 r 1 = 5 ln ⁡ 20   m m 15   m m = 17,38   m m

E agora podemos calcular a excentricidade entre o centroide e a linha neutra:

e = r - - R = 17,5 - 17,38 = 0,12   m m

Passo 3

As tensões são dadas por

σ = M ( r - R ) A e r

A tensão está em sentido horário, então:

M = - 2,8   N m

Para região inferior da viga

σ 1 = M r 1 - R A e r 1

σ 1 = - 2,8   N m ⋅ 15   m m - 17,38   m m 37,5   m m 2 ⋅ 0,12   m m ⋅ 15   m m

σ 1 = 98,73   M P a

a região superior da viga está sobre compressão:

σ 2 = M r 2 - R A e r 2

σ 2 = - 2,8   N m ⋅ 20   m m - 17,38   m m 37,5   m m 2 ⋅ 0,12   m m ⋅ 20   m m

σ 2 = - 81,51   M P a

Resposta

σ 1 = 98,73   M P a

σ 2 = - 81,51   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o caso geral de uma viga prismática sujeita às componentes de momento fletor Mye Mz, como mostra a figura, quando os eixos x, y, z passam pelo centroide da seção transversal. Se o material f
Três placas de aço de 120m m × 10m m foram soldadas para formar a viga mostrada na figura. Considerando que o aço seja elastoplástico com E = 200G P a e σ E = 300M P a , determine ( a ) o momento flet
As quatro forças mostradas na figura abaixo são aplicadas a uma placa rígida suportada por um poste de aço cheio de raio a . Sabendo que P = 100k N e a = 40m m , determine a tensão máxima no poste qua
Três pranchas de madeira são conectadas com parafusos de 14 mm de diâmetro espaçados a cada 150 mm ao longo do eixo longitudinal da viga. Para uma força cortante vertical de 10 kN, determine a tensão
Uma viga com a seção transversal mostrada na figura está submetida a um momento M 0 que atua em um plano vertical. Determine o maior valor admissível do momento M 0 se a tensão máxima na viga não deve