Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 116

Usando as técnicas descritas no Apêndice A, Exemplo A.5 ou A.6, a seção em Z tem momentos principais de inércia Iy= 0,060(10-3)m4 e Iz= 0,471(10-3)m4, calculados em torno dos eixos principais de inércia y e z, respectivamente. Se a seção for submetida a um momento interno

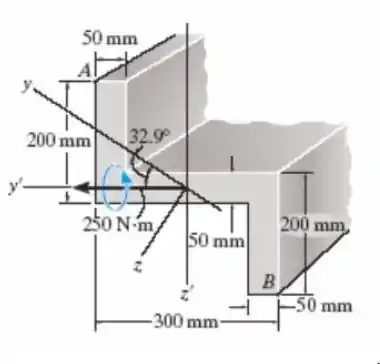
M = 250 N · m direcionado na horizontal, como mostra a figura, determine a tensão produzida no ponto B.

Passo 1

Faaaala, meu povo bonito!! Tudo bem com vocês??

A questão de hoje tem essa cara meio estranha e formal, mas ele enrolou só pra dizer que os momentos de inércia, nos eixos y e z, são aqueles dados, e um momento M foi aplicado formando um ângulo de 32,9º em relação ao y com a horizontal.

Depois desse monte de número, vamos determinar a tensão no ponto B. E aí, preparados?? Bora lá

Passo 2

A ideia aqui é decompor esse momento em y ' nos eixos dos momentos principais y e z . Aí a gente pode usar a fórmulinha de momentos que a gente já conhece, só que em relação aos eixos y e z .

Isso porque essa fórmulinha só pode ser usada quando usamos os dados em relação aos eixos principais de uma peça. (quando há simetria, esses eixos são os eixos de simetria)

M y   =   250 . c o s ( 32,9 º )   =   209,9   N . m

M z   =   250 . s e n ( 32,9 º )   =   135,8   N . m

Prontinho. E ele já deu os momentos nesses eixos:

I y = 0,06   10 - 3   m 4  

I z = 0,471 10 - 3 m 4

Passo 3

Se liga lá na fórmula:

σ   =   ( y   M z ) ( I z )     +   z   M y ( I y )  

Tá tudo positivo porque o momento M causa tração em A .

Falta a gente achar as posições de B em relação aos eixos principais.

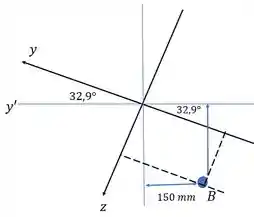
Podemos acha-las assim então:

y   =   0,15 . c o s ( 32,9 º )   –   0,175 . s e n ( 32,9 º )   =   0,2210   m

z   =   0,15 . s e n ( 32,9 º )   –   0,175 . c o s ( 32,9 º )   =   - 0,06546     m

Passo 4

Agora que já temos os momentos e posições necessárias, vamos jogar lá na fórmula:

σ   =   ( y ' M z ' ) ( I z ' )     +   z ' M y ' ( I y ' )       =   293 k P a

Resposta

σ   =   293 k P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a barra curva e o carregamento mostrado, determinar o percentual de erro introduzido no cálculo da tensão máxima, assumindo-se que a barra é reta. Considerar o caso quando: r = 5m m r = 25m m r =
Uma conexão de aço tem a seção transversal mostrada e os furos estão dispostos segundo o ângulo central β . Sabendo-se que a tensão admissível é de 100M P a , determinar a maior força P que pode ser a
Para a barra curva e o carregamento mostrado, determinar o percentual de erro introduzido no cálculo da tensão máxima, assumindo-se que a barra é reta. Considerar o caso quando: r = 5m m r = 25m m r =
Considerando que o momento mostrado é substituído por uma força vertical de 10 kN aplicada no ponto D e no sentido descendente, determinar a tensão (a) ponto A; (b) ponto B
Para o gancho mostrado, determinar a maior tensão na seção a-a, quando b 1 = 35m m e b 2 = 25m m