Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 31
31. Para a viga e o carregamento mostrados nas figuras, (a) trace os diagramas de esforço cortante e de momento fletor, (b) determine os valores absolutos máximos do esforço cortante e do momento fletor.
Passo 1
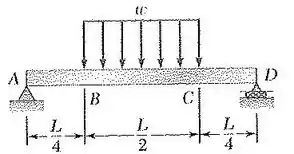
Bom! Vamos dar uma olhadinha na figura do enunciado e ver onde podemos começar nossa análise:
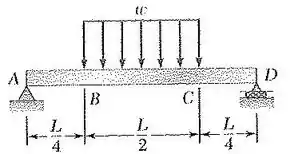
Olha só! Se você está em dúvida em relação ao que é esse presente na figura, saiba que essa letrinha é característica de uma coisa muito comum nos problemas de estática, em situações de carregamento distribuído.
Só que nesse caso, como o carregamento distribuído se assemelha a um retângulo, a força total produzida por ele, vai ser dada por:
No caso da figura do enunciado, temos que o comprimento do carregamento vai ser . Logo:
A próxima coisa agora, vai ser descobrir as reações, que obviamente vão estar em e em . Aí você já deve estar pensando. Partiu fazer diagrama de corpo livre, somatório de força e momento, dentre essas coisas que estamos acostumados a fazer.
Só que não!!! Repara na figura do enunciado. Dá pra notar que e são simétricos, se traçarmos uma linha passando pelo ponto médio da viga, né não!? Ora bolas! Se e são simétricos, então as forças de reação serão também. Isso quer dizer que essas forças, que chamaremos de e terão a mesma magnitude, de modo que podemos obtê-las simplesmente fazendo o somatório das forças no eixo :
Mas como :
Passo 2
Descobertas as forças de reação em e , temos que nos dedicar a obtenção dos esforços cortantes e momentos fletores. Para fazer isso, já sabe; né!? Temos que separar a viga em vários trecho e analisá-los separadamente, com nosso estudo indo do ponto até o :
Bora lá!! O primeiro trecho é o , e o diagrama de corpo livre para esse trecho está logo abaixo:
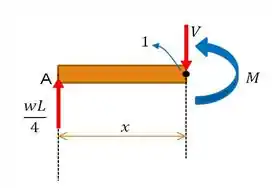
Diante dessa belezinha de imagem, fica até fácil saber o que temos fazer. Ora bolas! Para achar o esforço cortante, basta fazer o somatório das forças em . Olho lá, na nossa convenção adotada do esforço cortante, para baixo:
E para achar o momento fletor, tá vendo aquele ponto que nomeamos de na nossa figura. Pois bem! Vamos fazer o somatório dos momentos em relação a ele:
Pronto! Finalizamos o trecho , que vai de até :
Passo 3
Agora, bora partir pro trecho , com a nossa análise agora, indo de até . Para isso, bora lá fazer o esboço do nosso problema:
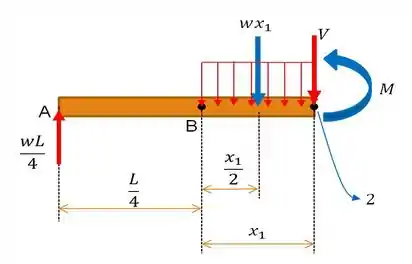
E como ninguém aqui é papagaio, bastar realizar os mesmos procedimentos do . Primeiro, o somatório das forças em :
Ah! Antes que alguém pergunte, esse vai de até ; que é o comprimento do trecho :
Depois, façamos o somatório dos momentos em relação ao ponto que nomeamos de . Olho lá nas distâncias entre as forças, hein!?
Esses são os valores que obtivemos para o trecho :
Passo 4
a) Ainda falta fazer o cálculo para o trecho , né não! Ai que chato!
E se eu disser que não precisa!! Isso mesmo que você ouviu!! Uma vez que os pontos e são simétricos; podemos dizer que os trecho e , também são, correto? Isso quer dizer que ao traçar os gráficos de esforço cortante e momento fletor, para o trecho ; os gráficos que teremos que traçar para o trecho são o inverso disso.
Desse jeito; a melhor forma de resolver este item é traçar os gráficos para o trecho , e quando chegar no trecho , apenas fazer a inversão do que obtivemos em :
Baseado nisso; bora lá pro que interessa. Vamos calcular alguns pontos de interesse para construir o nosso gráfico:
Para o trecho :
Para o trecho :
Com esses dados, tratemos de construir o gráfico, lembrando de que no trecho , o gráfico vai ser simétrico a :
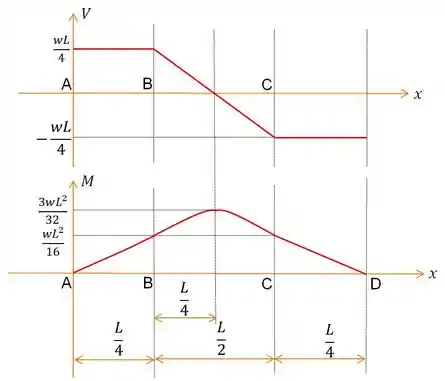
Passo 5
b) Finalmente, como a questão nos pede para determinar os valores absolutos máximos do esforço cortante e do momento fletor, o que temos que fazer nesse caso, é simplesmente usar a visão e ver qual o maior valor em módulo podemos extrair dos gráficos.
Trata-se portanto, de uma coisa simples e ao observar a figura do , notamos que nossas respostas são dadas por:
Resposta
a)
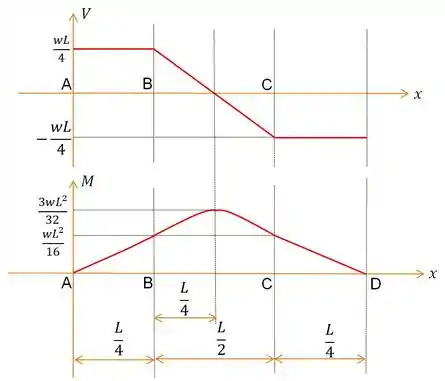
b)