Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.6 - Ex. 103
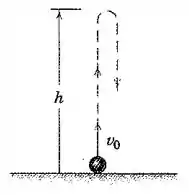
Utilize o método de trabalho-energia para desenvolver uma expressão para a altura máxima atingida por um projétil que é lançado com velocidade inicial a partir do nível do solo. Avalie sua expressão para . Assuma uma aceleração gravitacional constante e despreze a resistência do ar.
Passo 1
Beleza, galera? Na situação do problema, a gente tem a força peso como a única agindo sobre o projétil. Essa força tem módulo constante, a mesma direção do movimento e sentido contrário, e portanto o trabalho realizado até a altura máxima será:
Mas lembre-se que esse trabalho também é igual a variação da energia cinética, certo?
Na altura máxima , temos , logo:
Passo 2
Agora vamos avaliar nossa expressão para , sendo :
Resposta
Exercícios de Livros Relacionados
No projeto de um sistema de esteiras transportadoras, pequenos blocos metálicos são descarregados com uma velocidade de 0,4m / s sobre uma rampa pela esteira transportadora superior mostrada. Se o coe
O cursor de 2k g é liberado a partir do repouso em A e desliza para baixo a haste fixa inclinada no plano vertical. O coeficiente de atrito dinâmico é 0,4 . Calcule(a) a velocidade v do cursor quando
O cursor A de 15k g é liberado a partir do repouso na posição mostrada e desliza com atrito desprezível para cima na haste fixa inclinada de 30 ° em relação à horizontal sob a ação de uma força consta
O carrinho de montanha-russa tem massa de 800 kg, incluindo seus passageiros, e parte do topo da estrutura A com uma velocidade Va = 3 m/s. Determine a altura mínima h da estrutura de maneira que o ca
O carrinho de montanha-russa tem massa de 800 kg, incluindo seus passageiros. Se ele é solto do repouso no topo da estrutura A, determine a altura mínima h da estrutura de maneira que o carrinho dê a