Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.6 - Ex. 116
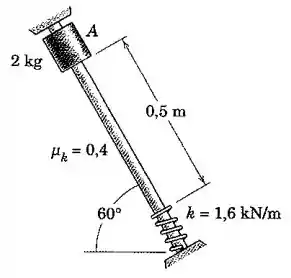
O cursor de é liberado a partir do repouso em e desliza para baixo a haste fixa inclinada no plano vertical. O coeficiente de atrito dinâmico é . Calcule
(a) a velocidade do cursor quando este colide com a mola e
(b) a deflexão máxima da mola.
Passo 1
(a) Primeiramente, observe o seguinte diagrama de forças sobre o cursor, que faz um movimento de descida como se fosse num plano inclinado:
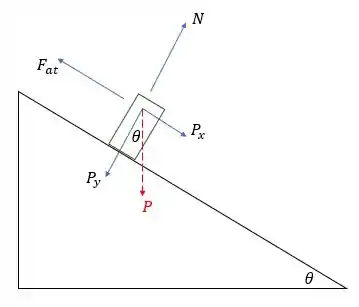
Na direção perpendicular à superfície, a componente do peso e a normal se equilibram, de modo que:
Na direção paralela à superfície, a outra componente do peso e a força de atrito atuam, de modo que a força resultante é:
Passo 2
Sabendo da força resultante na direção do movimento, calculamos o trabalho total:
Por outro lado, a variação de energia cinética será:
Como a variação da energia cinética de um corpo é igual ao trabalho total realizado sobre ele, temos:
Passo 3
(b) Quando o cursor colide com a mola, ele também passa a sofrer uma força contrária a seu movimento, a força elástica. Sendo assim, o trabalho realizado por todas as forças (incluindo o trabalho da força elástica) ao longo de toda a distância será:
Como o cursor parte do repouso e volta ao repouso quando comprime a mola ao máximo, a sua variação de energia cinética é nula, então:
Desprezando a solução negativa da equação do segundo grau acima, obtemos:
Resposta
(a)
(b)