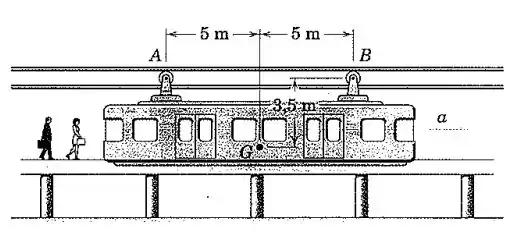
Um vagão de passageiros de um sistema suspenso de monotrilho é acionado por uma de suas duas pequenas rodas A ou B. Selecione a roda para a qual o vagão pode receber a maior aceleração sem deslizamento da roda motriz e calcule a aceleração máxima se o coeficiente de atrito efetivo é limitado a 0,25 entre as rodas e o trilho. Despreze a pequena massa das rodas.

Pessoal, primeiro vamos fazer o diagrama de corpo livre. Sabemos que o vagão está acelerado para a direita e que as forças atuantes no sistema são o peso do vagão, as reações nas rodas A e B e o atrito da roda motriz.

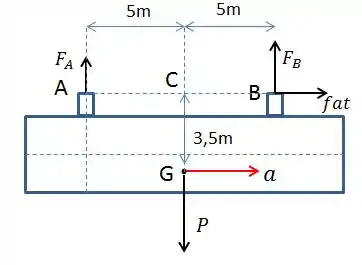
Para descobrir a roda motriz, temos que verificar qual roda possui a maior componente normal, pois . Para isso, vamos usar a equação de momento em relação ao ponto C:

Portanto, temos que , sendo B a roda motriz (onde atuará o atrito). Então o máximo atrito será:

Agora, vamos usar as equações de equilíbrio do sistema.

Temos um sistema com as equações (1), (2) e (3). Pegando a 1 e 2, temos:

Substituindo na equação 3: