Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 66
A variação no diâmetro de um grande parafuso de aço é cuidadosamente medida enquanto a porca é apertada. Sabendo que , determine a força interna no parafuso, quando se observa que o diâmetro diminui em .
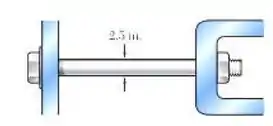
Passo 1
Para determinarmos a força interna no parafuso, quando se observa que o diâmetro diminuir em , vamos resgatar as informações acima: Agora podemos determinar a deformação em y, vejam:
Então podemos determinar a tensão exercida na peça:
Calculando a área temos:
Agora simmm gurizada podemos determinar a força , aplicando na equação abaixo:
Resposta
Exercícios de Livros Relacionados
Uma haste tem raio de 10mm . Se for submetida a uma carga axial de 15N tal que a deformação axial na haste seja ϵ x = 2,75 ⋅ 10 - 6 , determine o módulo de elasticidade E e a mudança em seu diâmetro.
A haste é feita de alumínio 2014 -T 6 . Se for submetida à carga de tração de 700N e tiver diâmetro de 20mm , determine a deformação por cisalhamento máxima absoluta na haste em um ponto sobre sua sup
Determine o módulo de compressibilidade para borracha dura se E b = 5GPa e ν b = 0,43 .
As tensões principais no plano e as deformações associadas em um plano em um ponto são σ 1 = 250MPa , σ 2 = 112MPa , ϵ 1 = 1,02 ( 10 - 3 ) , ϵ 2 = 0,180 ( 10 - 3 ) . Determine o módulo de elasticidade
O vaso de pressão esférico tem diâmetro de 2 m e espessura de 10 mm. Um extensômetro com 20 mm de comprimento é ligado ao vaso e constata-se um aumento no comprimento de 0,012 mm quando o vaso é press