Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 10.Problemas - Ex. 48
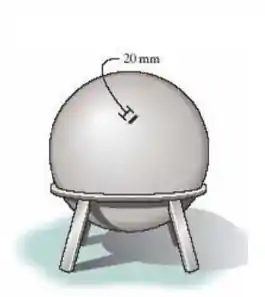
O vaso de pressão esférico tem diâmetro de 2 m e espessura de 10 mm. Um extensômetro com 20 mm de comprimento é ligado ao vaso e constata-se um aumento no comprimento de 0,012 mm quando o vaso é pressurizado. Determine a pressão que provoca essa deformação e calcule a tensão de cisalhamento máxima no plano e a tensão por cisalhamento máxima absoluta em um ponto sobre a superfície externa do vaso. O material é aço, para o qual e
Passo 1
Fala aí pessoal. Bora pra mais um problema.
Primeiramente, vamos calcular a tensão máxima em função de alguns parâmetros dados:
Se substituirmos os valores conhecidos, ficaremos com:
Agora, podemos também calcular a deformação máxima:
Passo 2
O próximo passo é calcular o p através da fórmula da deformação. Como temos os valores da fórmula, podemos isolar o :
Isolando-se o , ficaremos com:
Agora, é só voltar na expressão achada no primeiro passo e determinar a tensão máxima:
Podemos também calcular a tensão máxima no plano mas nesse caso ela será nula porque a tensão é uma tensão principal:
A tensão máxima absoluta será:
Deixando claro que o nosso foco aqui não é treinar contas, mas a teoria. Logo, as operações foram simplificadas.