Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 66

Várias forças são aplicadas ao tubo mostrado. Sabendo-se que o tubo tem diâmetro, interno e externo, de 40 mm e de 48 mm, respectivamente, determinar as tensões normal e de cisalhamento no: (a) ponto H; (b) ponto K.

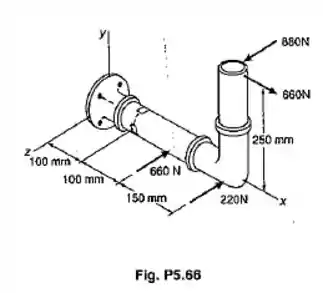
Passo 1

Do enunciado temos

d i n t = 40   m m

d e x t = 48   m m

Com isso podemos calcular A, J e I.

A = π 0,024 2 - 0,02 2 = 5,529 × 10 - 4 m 2

J = π 2 0,024 4 - 0,02 4 = 2,698 × 10 - 7 m 4

I = π c 4 4 = π × 0,024 4 4 - π × 0,02 4 4 = 1,349 × 10 - 7 m 4

Passo 2

Vamos agora fazer uma análise rápida dos momentos nos eixos

M x = 880 × 0,25 = 220   N m

M y = 660 × 0,1 + 220 × 0,25 - 880 × 0,25 = - 99 N . m

M z = 660 × 0,25

σ H = P A + M c I = 0 + 600 × 0,04 2010619,3 × 10 - 12 = 11936,62   M P a

τ H = 600 × 0,04 4021238,6 × 10 - 12 = 5968,31   M P a  

Passo 3

Com isso podemos começar as continhas

σ H = P A + M c I = 600 5,529 × 10 - 4 + 165 × 24 × 10 - 3 1,349 × 10 - 7 = 30,549   M P a  

σ K = P A + M c I = 600 5,529 × 10 - 4 + - 99 × 24 × 10 - 3 1,349 × 10 - 7 = - 16,419   M P a  

τ H = τ K = T c J = 220 × 24 × 10 - 3 2,698 × 10 - 7 = 19,57   M P a  

Resposta

a )   σ H = 30,549   M P a  

τ H = 19,57   M P a  

b )   σ K = - 16,419   M P a  

τ K = 19,57   M P a  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a variação na altura d de uma em balanço que suporta uma força concentrada P em extremidade, de modo que ela tenha uma tensão de flexão máxima constante σ a d m em todo o seu comprimento. A
Trace os diagramas de força cortante e momento fletor para o eixo e determine, com aproximação de múltiplos de 5mm, o diâmetro exigido se σ a d m = 50M P a e τ a d m = 20 M P a . Os mancais em A e D e
Trace os diagramas de força cortante e momento fletor para o eixo e determine, com aproximação de múltiplos de 5mm, o diâmetro exigido se σ a d m = 50M P a e τ a d m = 20 M P a . Os mancais em A e D e
A viga mostrada na figura suporta uma força concentrada P e seu centro. Se for feita de uma chapa com largura constante b , determine a tensão de flexão máxima absoluta na viga
A viga com avanço foi construída com duas peças de madeira de 50 mm por 100 mm escoradas como mostra a figura. Se a tensão de flexão admissível for σ a d m = 4,2M P a , determine a maior carga P que p