Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 11.Problemas - Ex. 31
A viga mostrada na figura suporta uma força concentrada P e seu centro. Se for feita de uma chapa com largura constante , determine a tensão de flexão máxima absoluta na viga
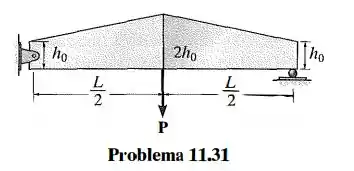
Passo 1
Vamos observar a viga e a seção transversal:
Pra resolver essa questão basta aplicar a equação da flexão. A única diferença será determinar uma equação que represente o momento de inércia e o ponto de aplicação do momento, já que a altura da viga é variável.
Outra coisa a se notar é a seguinte: já que o momento de inércia varia, não podemos garantir que a tensão máxima ocorrerá no meio da viga! Então como iremos determinar este ponto?
- Encontramos as reações de apoio
- Encontramos uma equação para o momento fletor M(x)
- Encontramos uma equação para o momento de inércia I(x)
- Aplicamos a equação da flexão
- Derivamos e igualamos a equação da flexão a zero para encontrar o ponto de máximo
Para facilitar nossas contas, vamos levar em consideração que a viga é simétrica, e consequentemente seus esforços e tensões são simétricos. Então faremos todos esses cálculos apenas para uma metade da viga!
Passo 2
Como esta viga é perfeitamente simétrica, com apoios simétricos e força centralizada, as reações de apoio são:
Passo 3
Vamos gerar equações para os esforços internos para a primeira metade da viga
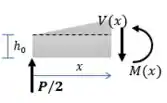
Passo 4
Vamos definir as equações que representem as propriedades geométricas da viga:
Passo 5
Mas também é preciso definir: Qual é o comportamento de ?
Por simplicidade, vamos olhar um dos lados da viga:
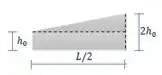
Observando a viga sabemos que é uma função linear
E que varia entre:
Vamos resolver esse sistema:
Assim, a função que representa a altura é:
Em evidência:
Passo 6
Pronto! Agora só aplicar na equação da flexão
Substituindo :
Passo 7
Para encontrar o ponto máximo vamos derivar e igualar a zero a equação da flexão:
Joga o denominador pro outro lado:
Botamos algumas constantes em evidência:
E jogamos pro outro lado:
Vamos colocar em evidência:
Dessa situação temos duas hipóteses
Assim, o ponto de máxima tensão é:
Passo 8
Pra finalizar, aplicamos o valor de na equação da flexão