Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 128
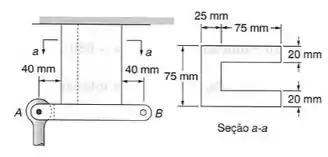
Uma barra vertical é articulada no ponto A do suporte de ferro fundido mostrado. Sabendo-se que as tensões admissíveis do suporte são e , determinar a maior força orientada para baixo, e a maior orientada para cima, que pode ser exercida pela barra.
Passo 1
Nosso objetivo é determinar a carga P máxima que pode ser aplicada a nossa seção tanto quando ela for orientada pra baixo, quando ela for orientada pra cima. Sabemos que a tensão pode ser definida pela seguinte equação:
- Carga orientada pra cima (compressão)
- Carga orientada pra baixo (tração)
Precisamos da LN para determinarmos tudo que precisamos, momento fletor, o valor de y e o valor do momento de inércia, com isso podemos seguir o seguinte passo a passo para termos a LN:
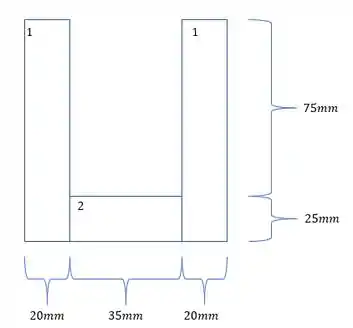
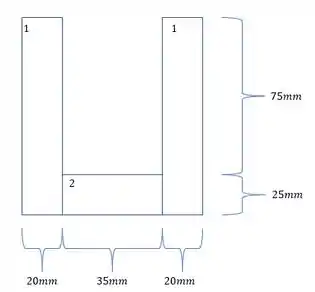
- Vamos dividir em seções mais simples, e numerar elas:
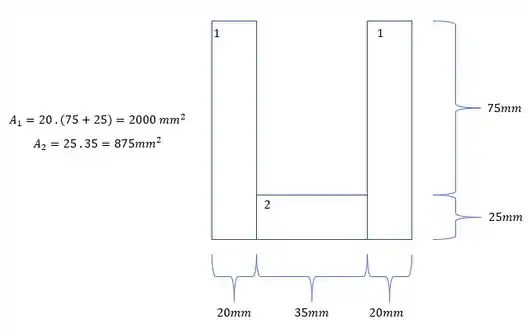
- As áreas são:
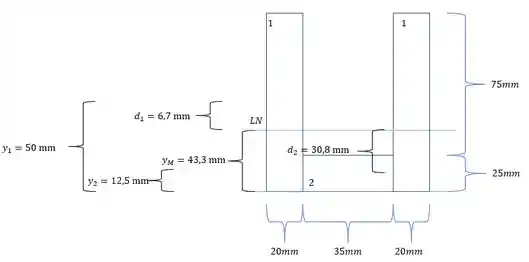
- Em terceiro, precisamos determinar uma origem, porque vai ser com relação com essa origem que vamos determinar a distância dos centroides de cada um dos elementos mais simples. Eu geralmente uso a base do elemento como origem, sendo assim teremos que:
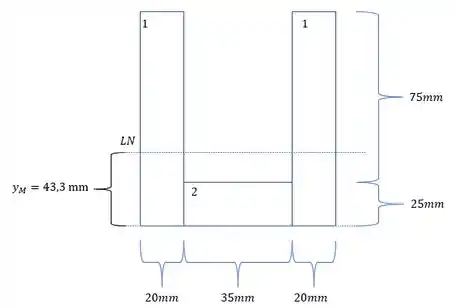
- Por fim precisamos usar a seguinte fórmula para determinar a LN, sendo assim teremos que:
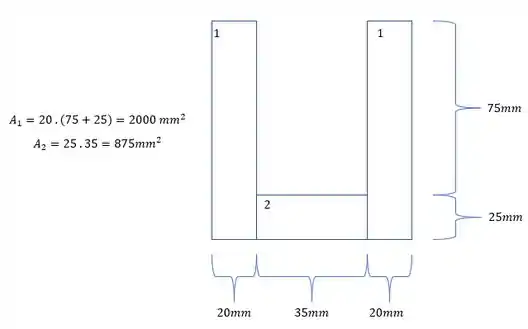
Com isso teremos que:
Substituindo teremos que:
E assim temos que:
Passo 2
Vamos definir primeiro o momento de inércia e y teremos que:
-
Para ele precisamos fazer a seguinte relação.
- Numeração das regiões
- Área das regiões
- Distância do centroide das áreas até a LN – aqui que vamos precisar da nossa LN
- Momento de inércia de cada região
Olha como esse macetinhos nos ajuda bastante.
- positivo e negativo
- Momento gerado pela carga para cima
- Momento gerado pela carga para baixo
- Carga P quando a carga está orientada para baixo
- Carga P quando a carga está orientada para cima
Agora para determinarmos o momento de inércia, precisamos fazer a seguinte conta:
Mas temos que lembrar que precisamos usar os valores de inercia da região 6 como negativa, sendo assim temos que:
Agora só precisamos determinar os valores de y, sendo assim teremos que ver o próximo passo.
Passo 3
Tendo o valor de y precisamos usar a tensão, sendo assim teremos que:
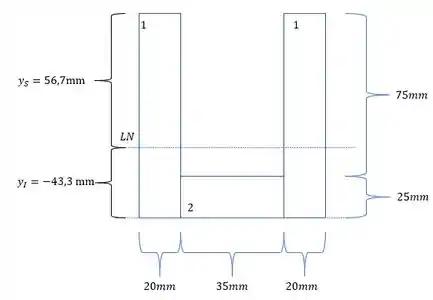
E para calculo de momentos fletores temos que detemrinar a excentricidade, sendo assim teremos que:
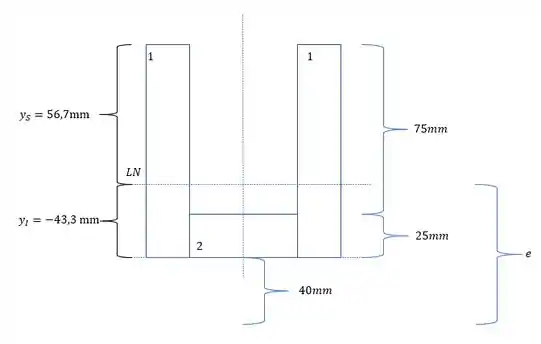
Vamos calcular primeiro o caso da carga para baixo.
Substituindo nas tensões teremos que:
Sabemos que a tensão admissível é dada por:
como o valor de P tem que ser positivo para que a conta seja coerente, não teremos compressão da seção, apenas tração, analisando então a tração da seção, teremos que:
Como queremos a máxima carga que pode ser aplicada, devemos tomar o cuidado de usarmos a menor carga, porque pense da seguinte maneira. Se usarmos a máxima carga, ela irá romper a menor seção, porém se usarmos a menor carga, ela irá manter tanto a maio tensão quanto a menor tensão, sendo assim teremos que:
Vamos calcular agora o caso da carga para cima.
Substituindo nas tensões teremos que:
Sabemos que a tensão admissível é dada por:
Como o valor de P precisa ser positivo, consideraremos a porção superior tracionando e a inferior comprimindo, assim teremos que:
Como queremos a máxima carga que pode ser aplicada, devemos tomar o cuidado de usarmos a menor carga, porque pense da seguinte maneira. Se usarmos a máxima carga, ela irá romper a menor seção, porém se usarmos a menor carga, ela irá manter tanto a maio tensão quanto a menor tensão, sendo assim teremos que:
Resposta
Resposta
Ei, a resposta está no passo a passo :)