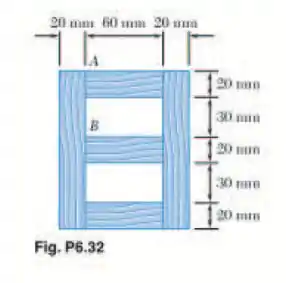
Várias pranchas de madeira são coladas para formar a viga de seção caixão mostrada. Sabendo que a viga está submetida a uma força cortante vertical de 3 kN, determine a tensão de cisalhamento média na junta colada (a) em A, (b) em B.

Tá legal! Vamos começar encontrando o momento de inércia para a seção. No nosso caso, vamos separar a seção da seguinte forma:

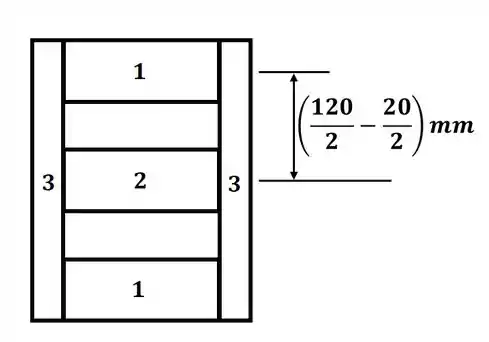
Note que já destacamos a distância entre o centroide da seção 1 e o centroide da seção transversal como um todo, pois vamos precisar dessa distância para usar o teorema dos eixos paralelos para essa seção. Sendo assim, o momento de inércia da seção 1 pode ser escrito como:

Agora, para encontrar o momento de inércia da seção 2, teremos:

E, por fim, para a seção 3, teremos:

Agora ficou fácil pra encontrar o momento total da seção, só somar os momentos encontrados, lembrando que temos duas seções “1” e duas seções “3”, então o momento total será:

Beleza! Agora vamos começar a encontrar os valores específicos para a letra (a). Como estamos interessados na junta do ponto A, a seção de interesse que teremos será:

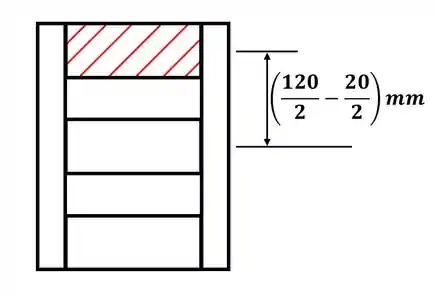
Então, para essa seção destacada, a área será:

Com isso, podemos encontrar o valor do momento de área, que é dado por:

Substituindo os valores conhecidos, temos:

Beleza! Quase lá! Agora precisamos da espessura t. Olhando para a figura, podemos ver que a seção A possui juntas do lado esquerdo e direito, então devemos somar esses dois comprimentos, ou seja:

Agora podemos utilizar a equação da tensão de cisalhamento, dada por:

E, substituindo os valores conhecidos, chegamos em:

Essa é a tensão de cisalhamento média na junta em A. Calma que não acabou, agora precisamos encontrar a tensão de cisalhamento média na junta em B.

Para a letra (b), vamos começar destacando a seção de interesse, então teremos:

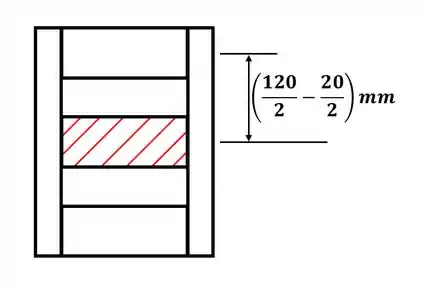
Então, para essa seção destacada, a área será:

Com isso, podemos encontrar o valor do momento de área, que é dado por:

Substituindo os valores conhecidos, temos:

Opa! Pera aí! Se o momento de área é igual a zero, olhando para a equação da tensão de cisalhamento a seguir:

Podemos ver que a tensão de cisalhamento será igual a zero para a junta em B:

E essa é a resposta da letra (b).