Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.3 - Ex. 24

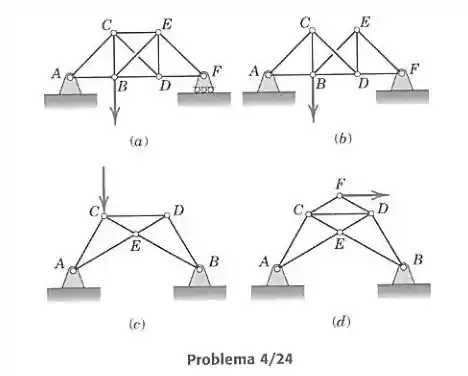
Verifique o fato de que cada treliça contém um ou mais elementos de redundância e proponha duas mudanças distintas, cada uma dais quais deve eliminar a redundância e gerar uma estrutura estaticamente determinada completamente. Todos os elementos podem suportar compressão e tração.

Passo 1

Uma treliça possui redundância quando há mais elementos do que o necessário para que ela não entre em colapso. Para que uma treliça seja estaticamente determinada, o número de equações que devemos ter deve ser igual ao número de incógnitas. Devemos ter 3 incógnitas para as forças externas (3 forças externas desconhecidas) e m incógnitas que correspondem às forças de cada um dos m elementos. Além disso, se temos j nós teremos 2 j equações, duas para cada nó, uma de equilíbrio no eixo x e uma para o equilíbrio no eixo y . Então a relação que deve ser satisfeita é:

m + 3 = 2 j

Passo 2

  1. Temos 10 barras ( m = 10 ) e 6 nós ( j = 6 ) , além de quatro forças externas desconhecidas, A x , A y e F y , pois F x = 0 . Então:

    2. m + 3 = 13 > 2 j = 12

    Temos mais elementos do que deveria, então devemos tirar uma barra. Tiramos a B E ou a C D .

    Passo 3

  2. Temos 9 barras ( m = 9 ) e 6 nós ( j = 6 ) , além de quatro forças externas desconhecidas, A x , A y , F x e F y . Então:

    3. m + 4 = 13 > 2 j = 12

    Podemos resolver o problema removendo uma equação externa, substituindo o apoio em A ou F por um apoio que produz apenas força vertical.

    Passo 4

  3. Temos 7 barras ( m = 7 ) e 5 nós ( j = 5 ) , além de quatro forças externas desconhecidas, A x , A y , F x e F y . Então:

    4. m + 4 = 11 > 2 j = 10

    Temos redundância no número de elementos e no número de forças externas. Removendo as barras A E ou B E , ficamos com a treliça determinada estaticamente, removendo também a redundância externa.

    Passo 5

  4. Temos 9 barras ( m = 9 ) e 6 nós ( j = 6 ) , além de quatro forças externas desconhecidas, A x , A y , F x e F y . Então:

m + 3 = 12 > 2 j = 10

Temos redundância no número de elementos e no número de forças externas. Removendo as barras A E ou B E , ficamos com a treliça determinada estaticamente, removendo também a redundância externa.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A treliça mostrada na figura consiste em seis elementos e é sustentada por uma pequena haste de conexão em A, duas pequenas hastes de conexão em B e por uma rótula em D. Determine a força em cada um d
99- Para a estrutura e carregamento mostrados na figura, determine a força exercida no elemento C F E em C e F .
104- Sabendo que P = 110N e Q = 250N , determine os componentes das forças exercidas a ) no elemento B C D F em C e D , b ) no elemento A C E G em E .
100- Para a estrutura e o carregamento mostrados na figura, determine a força exercida no elemento D C E em C e D .
102- Para a estrutura e carregamento mostrados na figura, determine os componentes de todas as forças atuantes no elemento A B E .