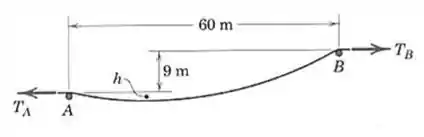
O cabo do problema 5/163 foi agora colocado sobre os suportes A e B cuja elevação difere de 9m, como mostrado. Faça um gráfico tanto da força trativa mínima quanto da força tativa nos apoios A e B em função de , para m onde é a deflexão abaixo do ponto A. Determine os três valores de força para h=2m e compare com os resultados do problema anterior. A massa do cabo, por unidade de comprimento, vale .

Temos que pela equação 5/19 para o B

Da mesma forma para o A:

E da equação 5/22 temos que:

Resolvendo a primeira equação numericamente e então aplicando para a segunda equação, obtemos o seguinte gráfico:

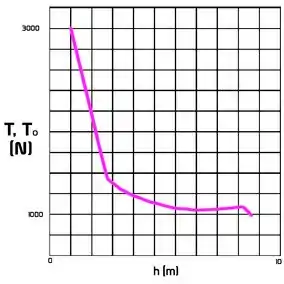
Para , e e