Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 22

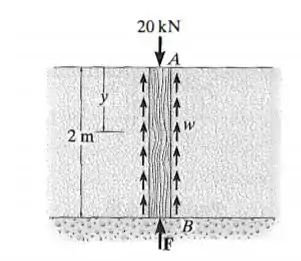
O poste é feito de abeto Douglas e tem diâmetro de 60   m m . Se estiver sujeito a uma carga de 20   k N e o solo proporcionar resistência ao atrito w   =   4   k N / m uniformemente distribuída ao longo de seus lados, determine a força F na parte inferior do poste necessária para haver equilíbrio. Calcule também qual é o deslocamento da parte superior do poste, A , em relação à sua parte inferior, B . Despreze o peso do poste.

Passo 1

Como o poste é feito de abeto Douglas temos que seu módulo de elasticidade é dado por E = 13,1   G P a . Desejamos encontrar o valor da força F e também qual o deslocamento da parte superior do poste em relação a parte inferior. Devemos lembrar que esse nosso deslocamento ( δ a - b ) vai ser dado por uma integral indo de 0 até o comprimento total do poste que é L .

Passo 2

Das equações de equilíbrio temos

∑ F y = 0 →   - P + w ⋅ L + F = 0 → F = 12 k N

Agora, se analisarmos as forças internas vamos ter

∑ F y = 0 → F y = - P + w ⋅ y  

Passo 3

Nosso alongamento vai ser dado por

∫ o L F y A ⋅ E   d y =   ∫ 0 L - P + w ⋅ y   d y π ⋅ 60 2 4 ⋅ 13,1 G P a = ∫ 0 2 - 20 k N + 4 k n m ⋅ y   d y π ⋅ 60 2 4 ⋅ 13,1 G P a ≈ - 0,864   m

Resposta

δ a - b = - 0,864 m   e   F = 12 k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A coluna de aço A- 36 tem área de seção transversal de 11250mm 2 e está revestida em concreto de alta resistência, como mostra a figura. Se uma força axial de 300kN for aplicada à coluna, determine a
O conjunto é formado por uma barra de alumínio A B C com 30mm de diâmetro com um colar fixo em B e uma haste de aço C D com 10mm de diâmetro. Determine o deslocamento do ponto D quando o conjunto for
O elo rígido é sustentado por um pino em A e dois cabos de aço A- 36 , cada um com comprimento de 300mm quando não alongados e área de seção transversal de 7,8mm 2 . Determine a força desenvolvida nos
A junta é composta por três chapas de aço A- 36 interligadas nas costuras. Determine o deslocamento da extremidade A em relação à extremidade B quando a junta for submetida às cargas axiais mostradas.
A coluna de aço A - 36 é usada para suportar as cargas simétricas dos dois pisos de um edifício. Determine as cargas P 1 e P 2 se A se mover 3m m para baixo e B se mover 2,25m m para baixo quando as c