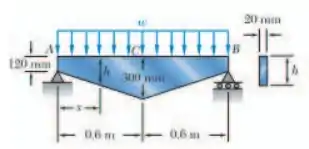
Para a viga de altura variável mostrada na figura, sabendo que , determine a seção transversal na qual ocorre a tensão normal máxima e o valor correspondente da tensão normal.

Para a altura variável da viga, temos que é uma reta em função de :

Onde é o coeficiente angular da reta, dado por:

Portanto:

Em seguida, vamos calcular o valor mínimo admissível do módulo de resistência da seção da viga. Para esta seção retangular, temos:

Em seguida, sabemos que a tensão normal admissível causada pelo momento fletor é dada por:

Substituindo:

E então, para encontrarmos o ponto de máxima tensão de flexão, temos que . Logo:

Agora, para determinarmos a seção transversal na qual ocorre a tensão normal máxima, basta determinarmos a posição , que é a distância do ponto até o ponto onde ocorre o momento máximo, através da equação que acabamos de encontrar. Temos:

Nesta parte, a gente não precisa considerar a a carga distribuída, pois a posição independe dela. Logo, podemos reescrever a equação assim

Isolando :

Subsituindo:

Assim, vamos utilizar esta posição de , para encontrarmos o valor da altura da viga. Fica assim:

Portanto, a nossa seção vai ser:

Por fim, para encontrarmos a tensão normal, vamos utilizar a relação da tensão causada pelo momento fletor. Ela é dada por:

Primeiro, sabemos que o valor mínimo admissível do módulo de resistência da seção da viga no ponto de flexão máxima que encontramos anteriormente é dado por:

Em seguida, vamos determinar o momento. Para isso, basta substituirmos na equação de momento fletor que a gente encontrou. Temos:

Agora que encontramos as variáveis das quais a tensão depende, basta substituirmos na sua fórmula:

É isso, galera! Bora fazer mais exercícios pra ficar craque.