Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 8.Problemas Revisão - Ex. 154
Para a viga em balanço com o carregamento mostrado, determinar a declividade e a deflexão em . Usar
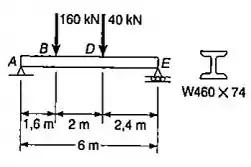
Passo 1
Fala aí galera, tudo bem? Bora pra mais uma questão de Resmat pra conseguir aquele notão na prova.
Neste exercício temos uma viga com dois apoios. Por isso, vamos utilizar o método da superposição para determinarmos a sua deflexão. Podemos dividí-la em dois casos:
Antes de entrarmos na parte legal da questão, temos que encontrar o momento de inércia para este perfil de viga , ele é tabelado e seu valor é de:
Agora, vamos lá no Apêndice do nosso livro, onde encontramos uma tabela de deformações das vigas de acordo com os tipos de carregamentos.
O primeiro carregamento, corresponde ao caso em que , logo, sua equação da linha elástica vai ser:
Opa, assim como no primeiro, o segundo carregamento também corresponde ao caso , porém, com. Logo:
Substituindo:
Com isso, temos que nossa deflexão em é dada pela soma das duas equações da linha elástica:
Passo 2
Em seguida, para encontrarmos a declividade no ponto , temos que derivar a equação da linha elástica fornecida no apêndice do nosso livro e, novamente, a soma dos dois casos de superposição é a declividade do nosso problema. Portanto:
É isso, pessoal