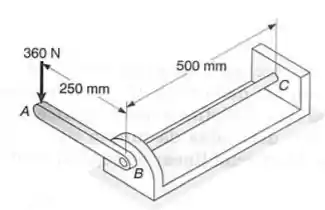
uma barra BC de diâmetro é firmemente fixada à alavanca e ao apoio C. A alavanca tem uma seção transversal uniforme de de espessura por de largura. Para o carregamento mostrado, determinar a deflexão no ponto A. Usar e .

Fala galerinha, para resolvermos esse problema vamos ter que lembrar de alguns conceitos que vão ajudar a gente no nosso cálculo. Não vai ser nada complexo, mas precisamos entender como o que aprendemos até aqui vai nos ajudar no cálculo da deformação no ponto A, para isso, podemos pensar o seguinte:

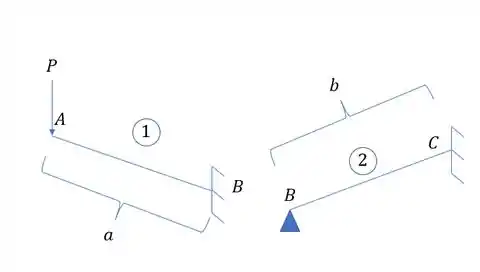
Perceba que dividi em duas vigas, porém perceba que considerei um engaste no ponto B, mas o ponto B não é um engaste, então vamos ter que calcular a deformação em A na viga 1 e depois transferimos as cargas para a viga 2 e calculamos o que acontece no ponto B, porque o que ocorrer em B vamos somar para saber o que rola em A, assim temos que:

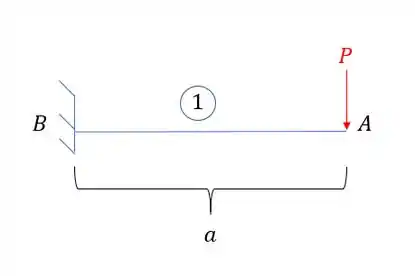
Assim a deformação em A é dada por:

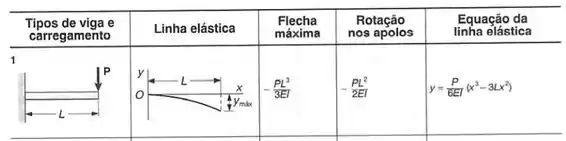
Agora podemos olhar a viga 2:

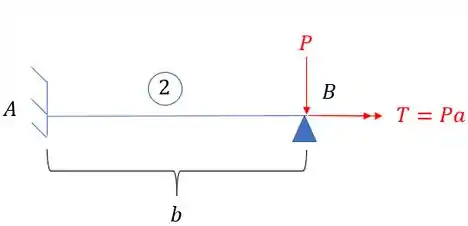
Perceba que transferimos na nossa carga para o ponto B, e podemos avaliar o seguinte, primeiro olhando a deformação da carga vertical, temos que como esse ponto possui um apoio, a deformação nele devido a carga vertical é:

E assim podemos dizer que a deformação para o ponto C será dada por:

E a deformação devido ao torque é dada por:

E para o torque temos que o calculo da deformação angular é dada por:

Sabemos que:

Assim a deformação total do ponto C vai ser a soma de todas as deformações que calculamos:

Sabemos pelo enunciado que:

Sabemos pelo enunciado que:

Substituindo, temos que: