Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 9.Problemas - Ex. 22
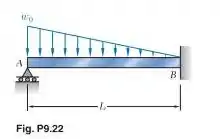
Para a viga e o carregamento mostrados nas figuras, determine a reação no apoio móvel.
Passo 1
Fala aí, galera. Tudo bem? Bora pra outra questão.
O primeiro passo desta questão é fazer um corte na estrutura, separando-a da seguinte maneira:
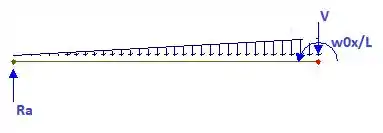
Precisamos da equação do momento na estrutura. Para isso, vamos usar algumas equações auxiliares:
No entanto:
Também sabemos que:
Por fim, o momento será:
Passo 2
Agora, com a equação do momento encontrada, basta substituir na equação da linha neutra e integrar duas vezes para acharmos a equação da linha elástica. Logo:
Integrando a primeira vez:
Esta é a equação da declividade. Para determinar vamos aplicar uma condição de contorno. Como a declividade no engaste é nula, teremos:
Integrando novamente:
Novamente, para achar vamos aplicar as condições de contorno. A deflexão no apoio é nula, logo:
Passo 3
Por fim, para achar a reação pedida, vamos aplicar outra condição de contorno. No engaste, a deflexão também é nula, logo:
Substituindo e arrumando:
Prontinho, reação determinada.