Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 9.Problemas de Revisão - Ex. 165

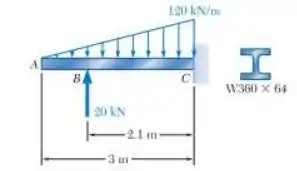
Para a viga em balanço e o carregamento mostrados, determine ( a ) a inclinação no ponto A , ( b ) a deflexão no ponto A . Utilize E = 200   G P a .

Passo 1

Fala aí, galera. Beleza? Vamos praticar mais mecânica pra tirar aquele 10 na prova.

Nesse problema temos que dividir as forças que geram momento em duas partes: a primeira para o carregamento distribuído e o segundo para a força que atua no ponto B .

Com isso, vamos desenhar os diagramas M / E I   para ambos. Para o primeiro, temos:

M 1 E I = 20 2,1 200 × 10 9 178 × 10 - 6 M 1 = 1,17978 × 10 - 3   m - 1

E então, vamos esboçar o diagrama:

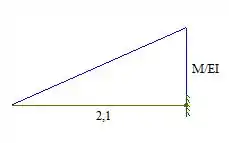
Assim, a área do diagrama vai ser:

A 1 = 1,23876 × 10 - 3

Vamos fazer o mesmo para o segundo carregamento:

M 2 E I = 1 2 1 20 3 1 200 × 10 9 178 × 10 - 6 M 2 = 5,0562 × 10 - 3   m - 1

E então, o diagrama vai ser:

E portanto, a área vai ser dada por:

A 2 = 1 4 3 - 5,0562 × 10 - 3 A 2 = - 3,7921 × 10 - 3

Passo 2

Com isso, podemos encontrar a inclinação em A a partir desta relação:

θ A = - θ C / A = - A 1 - A 2

Substituindo, dado que θ C = 0 :

θ A = 2,55 × 10 - 3   r a d

Passo 3

Por fim, a deflexão no ponto A vai ser dada por:

y A = t A / C

y A = A 1 3 - 0,7 + A 2 3 - 3 5 y A = - 6,25   m m

Resposta

θ A = 2,55 × 10 - 3   r a d

y A = - 6,25   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a reação no apoio móvel e a deflexão no ponto D se a = L 3 .
A barra rígida D E F é soldada no ponto D a uma viga laminada de aço A B . Para o carregamento mostrado, determine (a) a inclinação no ponto A , (b) a deflexão no ponto médio da viga em C . Utilize E
Determine a reação no apoio móvel e desenhe o diagrama de momento fletor para a viga e o carregamento mostrados nas figuras.
Determine a reação no apoio móvel e a deflexão no ponto D se a = L 3 .
Determine a reação no apoio móvel e a deflexão no ponto C .