Um tubo de alumínio com comprimento de e seção transversal de área de é soldado a um suporte fixo e a uma tampa rígida A barra de aço de de diâmetro, é soldada à tampa Sabendo que o módulo de elasticidade é de para o aço e para o alumínio, determine (a) a energia de deformação total do sistema quando e (b) a densidade de energia de deformação correspondente do tubo e na barra
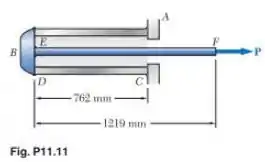
Passo 1
Fala aí, galera. Tudo bem? Bora pra outra questão.
Primeiramente, sabemos que a energia de deformação é dada por:
Pegando os trechos e calculando a área e substituindo os valores:
Passo 2
Agora, vamos determinar a densidade de energia de deformação, que é dada por:
Sabemos que:
Logo, substituindo os valores: