Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 122
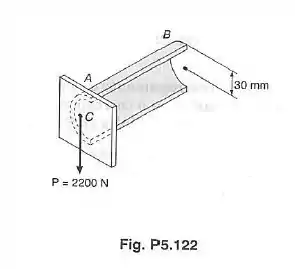
A viga em balanço consiste de metade de um tubo de parede fina, com raio médio de e espessura da parede de . Sabendo-se que a carga vertical passa através do centroide da seção transversal da viga, determinar: o torque que irá causar torção na viga sujeita a carga ; a máxima tensão de cisalhamento na viga causada pela carga .
Passo 1
Temos que determinar o torque que ira torcer nossa viga e a máxima tensão de cisalhamento na viga causada pela carga P.
Para torque, vamos determinar a distância correta do centro de cisalhamento e multiplicar pela nossa força de cisalhamento.
Para a máxima tensão de cisalhamento, teremos presente a tensão de cisalhamento de torção e flexão, a soma destas duas será nossa máxima tensão de cisalhamento.
Passo 2
a)Temos a seguinte situação:
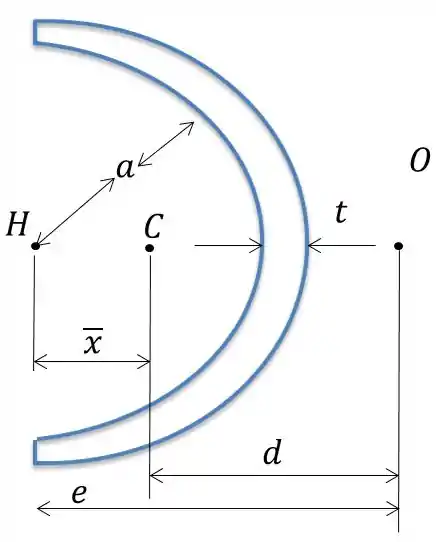
Calma, você já vai entender esse tanto de letras.
Seguinte !
Sabemos que a força passa pelo centroide do nosso tubo. Para determinar o torque de torção feito pela nossa tensão cisalhante , temos que saber a distância correta do centroide e do ponto de cisalhamento.
Como fazer isto ?
Bem vamos lá, como mostra na figura, temos que encontrar , definido por:
Para determinar , vamos encontrar o centro de cisalhamento :
O centro de cisalhamento de um semi-tubo, é definido por:
Caso você desejar ver está definição a resolução do exercício 5-113 terá o que você deseja.
E temos outra definição, para uma seção de metade de um tubo, a distância do centro ao centroide de um semi-tubo é:
Como temos e , basta determinar :
Como , vamos converter para metros(multiplicando por ), e substituindo em :
Utilizaremos este valor inteiro para afim de não termos muito erros pode arredondamento.
Passo 3
Agora para determinar o torque ficou simples, temos:
Como :
Passo 4
b) temos que determinar a tensão de cisalhamento por flexão e torção.
Vamos começar pela tensão por flexão:
Temos que determinar o momento de inércia e o momento estático .
Determinando o momento de inércia, para uma seção de circulo:
Em que:
A área de uma seção circular:
Substituindo em :
Substituindo em :
Como estamos lidando com metade de uma seção circular, temos:
Substituindo o raio e a espessura, em que multiplicando por para unidade ficar em metros, temos:
Passo 5
Já determinamos o momento de inércia, falta determinar o momento estático:
Que pode ser definido para uma seção de um semi-tubo, como:
Este cálculo você pode encontrar no nosso site solução do exercício 5-113.
Substituindo valores:
Passo 6
Finalmente podemos determinar a tensão de cisalhamento por flexão:
Substituindo todos os cálculos:
Passo 7
Para determinar a tensão de cisalhamento por torque ou torção, temos:
Temos , calculado na letra (a),
Temos que determinar e :
O termo é o somatório de todo o comprimento da viga, logo, o comprimento de um semi círculo é:
E possui uma fórmula definida por:
Substituindo todos os valores:
Como temos todas variáveis para determinar , basta substituir todas as variáveis:
Passo 8
Finalmente teremos a tensão cisalhante máxima:
Resposta
a)
b)