Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 50
O projeto de uma viga requer a soldagem de quatro placas horizontais à uma placa vertical de 12,7x127 mm como mostrado. Para uma força cortante vertical determinar a dimensão para que o fluxo de cisalhamento, através da superfície da solda, seja máximo.
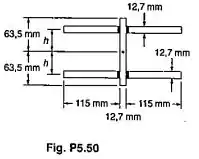
Passo 1
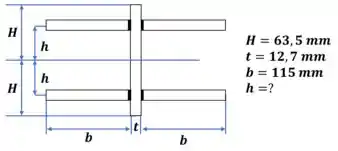
A figura é perfeitamente simétrica! Então o centroide dela é bem no meio da figura.
Isso facilita tudo, vamos calcular o momento de inércia da figura:
Passo 2
O nosso objetivo é calcular o momento o fluxo de cisalhamento na solda. Pra isso, a gente vai estudar uma das placas soldadas (destacada na figura)
O momento estático da região destacada é:
Passo 3
Agora vamos calcular o fluxo de cisalhamento:
A gente quer saber o ponto em que . Então, vamos derivar a equação e igualar a zero
A expressão pode parecer feia, mas dá pra ajeitar. Pra começar, vamos jogar o denominador pro outro lado:
Colocando em evidência e jogando pro outro lado:
Logo:
Assim, o ponto de máximo será: