Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 51

Determinar a tensão cisalhamento no ponto A de um tubo na parede fina como a seção transversal mostrada, casada por uma força cortante vertical V.

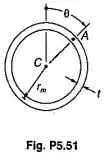
Passo 1

Pra começar, vamos calcular o momento de inércia da figura.

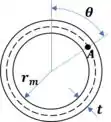
O momento polar de inércia de um anel é dado por:

J = A r m 2 J = 2 π r m t ⋅ r m 2 J = 2 π r m 3 t

E, por definição, o momento de inércia de área é metade do momento polar:

I = 1 2 ⋅ J I = π r m 3 t

Passo 2

Agora vamos calcular o momento estático. O momento estático desejado está destacado em laranja.

Primeiro precisamos calcular a área de uma seção circular:

A A = θ r m ⋅ t

O centroide de um arco circular é:

r c = r m sen ⁡ θ θ

Logo, o momento estático será:

Q A = A A ⋅ r c Q A = θ r m ⋅ t ⋅ r m sen ⁡ θ θ Q A = r m 2 ⋅ t ⋅ sen ⁡ θ

Passo 3

Agora é a parte mais fácil, vamos calcular a tensão no ponto A:

τ A = V Q A I t

τ A = V ⋅ r m 2 ⋅ t ⋅ sen ⁡ θ π r m 3 t ⋅ t

τ A = V sen ⁡ θ π r m t

Resposta

τ A = V sen ⁡ θ π r m t

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma força P de 5k N é aplicada a um arame, que é enrolado em torno da barra A B , como mostrado. Sabendo-se que a seção transversal da barra é um quadro de lado d = 40m m , determinar a tensão de cisa
Para a viga extrudada, com a seção transversal mostrada, determinar a localização do centro de cisalhamento O.
Para a viga extrudada, com a seção transversal mostrada, determinar a localização do centro de cisalhamento O.
Determinar a localização do centro de cisalhamento O, de uma viga de parede fina de espessura uniforme e com a seção transversal mostrada.
Para a viga extrudada, com a seção transversal mostrada, determinar a localização do centro de cisalhamento O.