Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 124

A viga cantilever de um quarto de círculo é submetida a uma pressão uniforme em sua superfície superior, conforme mostrado. A pressão é expressa em termos da força p por unidade de comprimento do arco circunferencial. Determine as reações na viga em seu suporte A em termos de compressão CA, cisalhamento VA e momento fletor MA

Passo 1

Nesta tarefa, precisamos determinar as reações em A.

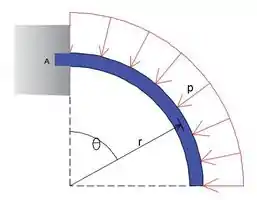
Diagrama do corpo livre

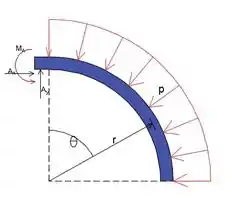
Passo 2

Primeiro, vamos considerar a condição de equilíbrio da força horizontal.

∑ F x = 0

A x - ∫ 0 π / 2   p r d ⁡ θ s i n ⁡ θ = 0 A x - p r ( - c o s ⁡ θ ) 0 π / 2 = 0 A x - p r ( - c o s ⁡ π / 2 + c o s ⁡ 0 ) = 0 A x - p r = 0 A x = p r

Vamos considerar a condição de equilíbrio da força vertical

∑ F y = 0

A y - ∫ 0 π / 2   p r d ⁡ θ c o s ⁡ θ = 0 A y - p r ⁡ ( - s i n ⁡ θ ) 0 π / 2 = 0 A y - p r ⁡ ( - s i n ⁡ π / 2 + s i n ⁡ 0 ) = 0 A y - p r = 0 A y = p r

Passo 3

Vamos considerar a condição de momento de equilíbrio sobre A

∑ M A = 0

M A - ∫ 0 π / 2   p r d ⁡ θ r s i n ⁡ θ = 0 M A - p r 2 ( - c o s ⁡ θ ) 0 π / 2 = 0 M A - p r 2 ( - c o s ⁡ π / 2 + c o s ⁡ 0 ) = 0 M A - p r 2 = 0 M A = p r 2

Resposta

A x = p r A y = p r M A = p r 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A treliça é composta de cinco membros, cada um tendo comprimento de 4m e massa 7k g / m . Se a massa das chapas de fixação nas juntas e a espessura dos membros puderem ser desprezadas, determine a dis
Localize o centroide x , y da seção transversal de metal. Desconsidere a espessura do material e as pequenas dobras nos cantos.
Localize  o  centro  de  gravidade  G ( x ,  y )   do  poste  de  iluminação.  Desconsidere  a  espessura  de  cada segmento. A massa por comprimento unitário  de cada segmento é a seguinte:  ρ A B =
Localize o centro de gravidade x ¯ , y ¯ , z ¯ do arame homogêneo.
O conjunto de placas de aço e alumínio é parafusado e preso ao muro. Cada placa tem uma largura constante na direção  z  de  200m m e espessura de 20 mm.  Se a densidade de  A  e  B  é  ρ a ç o = 7,85