Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 136

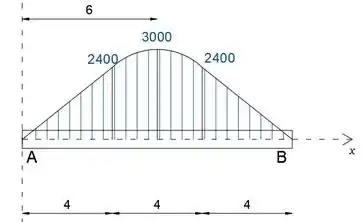
Desenhe os diagramas de cortante e momento para a viga carregada e determine o valor máximo M_max do momento.

Passo 1

Primeiro, vamos determinar as forças de reação do diagrama de corpo livre usando as equações de equilíbrio

Observe que substituímos a carga distribuída por sua resultante

R = 300 ⋅ 4 = 1200 l b

∑ M A = 0

1200 ⋅ 6 - 12 Y B = 0 Y B = 600 l b

∑ F x = 0

X A = 0

∑ F y = 0

Y A + Y B - 1200 = 0 Y A + 600 - 1200 = 0 Y A = 600 l b

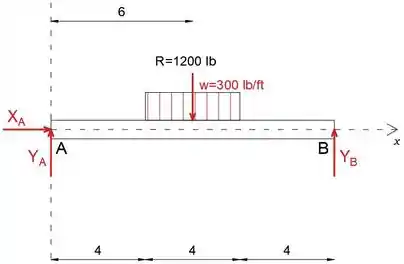
Passo 2

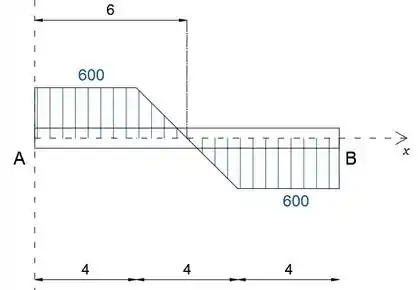
A partir daqui, podemos construir o diagrama de força cortante

Usando a fórmula V x = V x - 1 + Δ V , calcularemos as forças de cisalhamento da esquerda para a direita

V x = 0 = Y A = 600 l b V x = 4 = 600 + 0 = 600 l b V x = 8 = 600 - 300 ⋅ 4 = - 600 l b V x = 12 ← = - 600 + 0 = - 600 l b V x = 12 = - 600 + Y B = - 600 + 600 = 0

Observe que a força de cisalhamento está diminuindo linearmente ao longo da faixa 4≤x≤8 m, por causa da carga distribuída, enquanto ela tem dois "saltos" positivos em A e B e é constante no resto da viga

Como o diagrama é linear no intervalo [4≤x≤8], o momento máximo nesse intervalo está no ponto onde a força de cisalhamento é igual a zero. Como o diagrama é simétrico, podemos ver que a força cortante zero está em x = 6.

Passo 3

A seguir, usaremos o diagrama de força cortante para construir o diagrama de momento fletor

Uma vez que sabemos que o momento é igual a zero em x = 0 m, e que a mudança no momento é igual à área do diagrama de força cortante, então, usando a expressão M x = M x - 1 + Δ M , vamos calcular os valores do momento fletor nos pontos onde as forças externas atuam

M x = 0 = 0 M x = 4 = 0 + 600 ⋅ 4 = 2400 l b - f t M x = 6 = 2400 + 1 2 ⋅ 600 ⋅ 2 = 3000 l b - f t M x = 8 = 3000 - 1 2 ⋅ 600 ⋅ 2 = 2400 l b - f t M x = 12 = 2400 - 600 ⋅ 4 = 0

Observe que a inclinação para o diagrama de momento está diminuindo ao longo da faixa [4≤x≤6] e aumentando [6≤x≤8] enquanto é constante para o resto da viga, uma vez que a força cortante aumenta ao longo da faixa [4 ≤x≤6] e aumenta [6≤x≤8], enquanto é constante para o resto do feixe

Observe que o momento máximo, como dissemos na etapa acima, está em x = 6

M m a x = 3000 l b - f t '

Resposta

V x = 0 = 600 l b V x = 4 = 600 l b V x = 8 = - 600 l b V x = 12 ← = - 600 l b V x = 12 = - 600 + 600 = 0

M x = 0 = 0 M x = 4 = 2400 l b - f t M x = 6 = 3000 l b - f t M x = 8 = 2400 l b - f t M x = 12 = 0 M m a x = 3000 l b - f t   e m   x = 6 '

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Desenhe os diagramas de cisalhamento e momento para a viga simples carregada linearmente mostrada. Determine a magnitude máxima do momento fletor M.
A viga I suporta a força de 1000 lb e o par de 2000 lb-ft aplicado ao suporte de 2 pés soldado na extremidade da viga. Calcule o cisalhamento V e o momento M na seção intermediária entre A e B.
O quadro de ajuste da braçadeira de deslocamento especial suporte uma compressão de 500 N. Calcule a força cortante V, a tensão T e o momento fletor M na seção A da barra de braçadeira para x = 250 mm
Derive expressões para a força cortante V e o momento fletor M como funções de x na viga cantilever carregada como mostrado.
Desenhe os diagramas de cortante e momento para a viga de Prob. 5/116 repetido aqui e especifique o cisalhamento V e o momento M no comprimento médio da viga.