Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 12c

Para a viga com o carregamento indicado, considerar a seção n - n e determinar: (c) a maior tensão de cisalhamento.

Passo 1

Para achar a maior tensão de cisalhamento vamos fazer o seguinte:

  1. Calcular a força cortante da barra.
  2. Calcular onde a linha neutra se encontra.
  3. Calcular o momento de inércia da barra.
  4. Calcular o momento estático Q .
  5. Substituir na equação da tensão.

Passo 2

Vamos calcular a força cortante. Podemos ver que a força de 160   k N é aplicada exatamente no meio da barra, como não há outras forças então as reações nas bases serão:

R A = R B = 80   k N

Agora vamos fazer aquele desenho maneira de um corte dessa barra, vamos cortar exatemente em n :

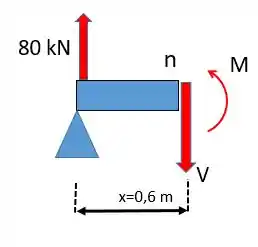
Para que a barra esteja em equilíbrio temos que ter:

- V + 80 = 0

V = 80   k N

Passo 3

Cálculo da linha neutra:

Y - = ∑ A ⋅ y - ∑ A

Aí, gente, se liga no macete monstro! A área da seção transversal é simétrica então nem precisa calcular a linha neutra, ela vai estar exatamente no meio da figura!

Y - = 80 + 100 + 80 2 = 130   m m

Passo 4

Agora vamos calcular o momento de inércia da barra, lembrando que ssa barra é composta por diversos retângulo podemos realizar da seguinte forma:

I = I 1 - 2 ⋅ I 2 - I 3

Lembrando que o momento de inércia de um retângulo é:

I = 1 12 ⋅ b ⋅ h ³

Vamos calcular I 1 como se a peça fosse toda maciça:

I 1 = 1 12 ⋅ 0,180 ⋅ ( 0,260 ) ³

I 1 = 2,6364 × 10 - 4   m 4

Agora I 2 é a parte relativa a cada vão superior e inferior:

I 2 = 1 12 ⋅ b ⋅ h 3 + A ⋅ d ²

I 2 = 1 12 ⋅ 0,180 - 2 ⋅ 0,012 ⋅ 0,080 3 + 0,180 - 2 ⋅ 0,012 ⋅ 0,080 ⋅ ( 0,050 + 0,040 ) ²

I 2 = 6,656 × 10 - 6 + 1,011 × 10 - 4

I 2 = 1,077 × 10 - 4   m 4

E I 3 o vão central:

I 3 = 1 12 ⋅ b ⋅ h ³

I 3 = 1 12 ⋅ ( 0,180 - 2 ⋅ 0,016 ) ⋅ ( 0,100 - 2 ⋅ 0,016 ) ³

I 3 = 3,878 × 10 - 6   m 4

Fazendo:

I = I 1 - 2 ⋅ I 2 - I 3

I = 2,6364 × 10 - 4   - 2 ⋅ ( 1,077 × 10 - 4 ) - 3,878 × 10 - 6

I = 4,436 × 10 - 5   m 4

Passo 5

Vamos calcular o momento estático Q . Agora, como queremos a maior tensão cisalhante vamos pegar a fibra da linha neutra, que ocorre em Y - = 130   m m se lembra?

Pegando a parte superior para o cálculo:

Q = ∑ A ⋅ Y -

Q = Q 1 - Q 2 - Q 3

Q 1 = 0,130 ⋅ 0,180 ⋅ 0,065

Q 1 = 1,521 × 10 - 3   m 3

Q 2 = 0,180 - 2 ⋅ 0,012 ⋅ 0,080 ⋅ 0,090

Q 2 = 1,1232 × 10 - 3   m 3

Q 3 = 0,180 - 2 ⋅ 0,016 ⋅ 0,050 - 0,016 ⋅ 0,050 - 0,016 2

Q 3 = 8,5544 × 10 - 5   m 3

Q = Q 1 - Q 2 - Q 3

Q = 1,521 × 10 - 3 - 1,1232 × 10 - 3 - 8,5544 × 10 - 5  

Q = 3,123 × 10 - 4   m 3

Passo 6

Agora vamos substituir na equação da tensão:

τ = V Q I t

Aqui falta só o termo t que representa a espessura da peça na linha que estamos observando, sendo assim:

t = 2 ⋅ 0,016   m

τ = 80000 ⋅ 3,123 × 10 - 4   4,436 × 10 - 5 ⋅ 0,032

τ = 17,6   M P a

Resposta

τ = 17,6   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Três tábuas, cada uma com 50 mm de espessura, são pregadas juntas para formar uma viga que é submetida a uma força cortante vertical. Sabendo-se que a força de cisalhamento admissível em cada prego é
Três tábuas são pregadas juntas para formar a viga mostrada, que é submetida a uma força cortante vertical. Sabendo-se que o espaçamento entre os pregor é s = 75 mm e que a força de cisalhamento admis
Resolver o Prob. 5.4, considerando que a largura é diminuída para w = 100 mm.
A viga mostrada foi fabricada com dois perfis de aço laminados e duas placas, unidos por parafusos de 20 mm de diâmetro e espaçados longitudinalmente de 190 mm. Determinar a tensão de cisalhamento méd
A viga composta mostrada é constituída de dois perfis de aço laminados W 150 x 29,8 unidades por parafusos de 16 mm de diâmetro e espagados longitudinalmente de 15 mm. Sabendo-se que a tensão de cisal