Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 9

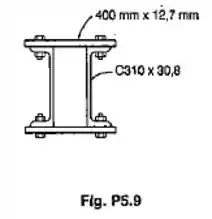
A viga mostrada foi fabricada com dois perfis de aço laminados e duas placas, unidos por parafusos de 20 mm de diâmetro e espaçados longitudinalmente de 190 mm. Determinar a tensão de cisalhamento média nos parafusos, causada pela ação de uma força cisalhante vertical de 110 kN.

Passo 1

D enunciado nós temos

d p a r a f u s o = 20   m m

V = 110   k N

s = 190   m m

Olhando na tabela para esse perfil temos

I x = 53,7 × 10 - 6 m 4

A = 3929   m m 2 = 0,3929 × 10 - 2 m 2

O y - será dado por

y - = 305 + 12,7 2 = 158,85   m m

Passo 2

Temos ainda para Q

Q = A × y - = 0,4 × 0,0127 × 0,15885 = 8 , × 10 - 4 m 3

Por ultimo ainda precisamos to momento de inércia total para aplicarmos a relação

H s = V Q I

Onde teremos para o momento de inércia

I z z = Σ I i + A i d i 2

I = I 1 + I 2 + I 3

Onde 1 representa o perfil central e 2 e 3 a barra superior e inferior.

I = 2 × 53,7 × 10 - 6 1 + 1 12 × 0,4 × 0,0127 3 + 0,4 × 0,0127 × 0,15885 2 2 + 1 12 × 0,4 × 0,0127 3 + 0,4 × 0,0127 × 0,15885 2 3

I z z = 3,639 × 10 - 4 m 4

Passo 3

Podemos então finalmente aplicar

H = V Q s I

H = 110 × 10 3 × 8,07 × 10 - 4 3,639 × 10 - 4 = 46,349   k N

Pra finalizar, tenha em emnte que estamos trabalhando com dois parafusos!

F p a r a f u s o = H 2 = 42,349 2 = 23,175   k N

Então

τ a d m = F p a r a f u s o A p a r a f u s o = 23,175 × 10 3 π × 0,01 2 = 73,768   M P a

Prontinho

Resposta

τ a d m = 73,768   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O perfil em U é submetido a um cisalhamento V = 75k N . Determine o fluxo de cisalhamento máximo no perfil.
A viga suporta um cisalhamento vertical V = 35k N . Determine a força resultante desenvolvida no segmento AB.
A escora de alumínio tem 10mm de espessura e a seção transversal mostrada na figura. Se for submetida a um cisalhamento V = 150N , determine o fluxo de cisalhamento nos pontos A e B.
O tubo está sujeito a uma força de cisalhamento V = 40k N . Determine o fluxo de cisalhamento no tubo nos pontos A e B
A viga é composta por quatro chapas e está sujeita a uma força de cisalhamento V = 25k N . Determine o fluxo de cisalhamento máximo na seção transversal.