Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 117

Para a viga com o carregamento indicado, determinar: (a) a declividade no ponto A; (b) a deflexão no ponto C. Usar E = 200 G P a .

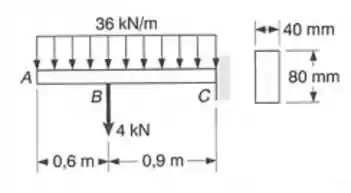
Passo 1

Vamos lá gurizada a mais um exercício de resmat :D

Considere que:

Unidades:Forças em kN, comprimento em m.

C a s o   6 :     W = 8 k n n ,   L = 3,9 m ,   x = 1,3 m

θ A = - w L 3 24 E I = - 8 3,9 3 24 E I = 19,773 E I

y c = - W 24 E I x 4 - 2 L x 3 + L 3 x = - 8 24 E I 1,3 4 - 2 3,9 1,3 3 + 3,9 3 1,3

= - 20,945 E I

Passo 2

Considerando que na C a r g a   I I               3 6 k N     c a r g a   c o n t r a d a   e m   C .     (   C a s o   5   d o   a p ê n d i c e   D )

P = 3 6 k N ,   L = 3,9 m ,       a = 1,3 m ,   b = 2,6 m ,   x = a = 1,3 m

θ A = - P b b 2 - b 2 6 E I L = - 3 6 2,6 3,9 2 - 2,6 2 6 E I 3,9 = - 32,861 E I

y x = - P a 2 b 2 3 E I L = 35 1,3 2 2,6 2 3 E I 3,9 = - 34,176 E I

Dados E = 200 × 10 9 ,   I = 102,0 × 10 6 m m 4 = 102,0 × 10 - 6 m 4

E I = 200 × 10 9 102,0 × 10 - 6 = 204 × 10 6 N ∙ m 2 = 20400 k N ∙ m 2

Passo 3

Agora sim podemos determinar o que foi pedido no enunciado :D

  1. Declive em A θ A = - 19,773 + 32,861 20400 = - 2,58 × 10 - 3 r a d

    2. θ A = 2,58 × 10 - 3 r a d

  2. D e f l e x ã o   e m   C         y c = - 20,934 + 34,176 20400 = - 2,70 × 10 - 3 m

y c = 2,70 m m ↓

Resposta

  1. - 2,58 × 10 - 3 r a d
  2. 2,70 m m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Cada elemento da treliça mostrada é feito de aço. A área da seção transversal do elemento B C é de 800m m 2 , e para todos os outros elementos a área é de 400m m 2 . Utilizando E = 200G P a , determin
Na treliça mostrada, todos os elementos são feitos do mesmo material e têm a área da seção trasnversal indicada. Determine a energia de deformação da treliça quando lhe é aplicada a força P .
Usando E = 73,1G P a , determine de forma aproximada a máxima energia de deformação que a barra de alumínio acumulará se a tensão normal admissóivel é σ a d m = 151,7M P a .
Cada barra de treliça mostrada na figura tem uma seção transversal uniforme de área A . Usando o método do trabalho e da energia, determine o deslocamento horizontal do ponto de aplicação da força P .
As barras de treliça mostradas na figura são feitas de aço e têm as áreas das seções transversais mostradas na figura. Usando E = 200G P a , determine o deslocamento vertical do nó C provocado pela ap