Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas - Ex. 71

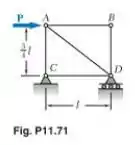
Cada barra de treliça mostrada na figura tem uma seção transversal uniforme de área A .   Usando o método do trabalho e da energia, determine o deslocamento horizontal do ponto de aplicação da força P .  

Passo 1

Fala aí, galera. Tudo bem? Bora pra outra questão.

Primeiramente, sabemos A B   e B D   não possuem forças, logo no nó A :

∑ F x = 0

4 5 F A D + P = 0

F A D = - 5 4 P

∑ F y = 0

- F A C - 3 5 F A D = 0

F A C = 3 4 P

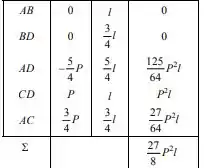
Resumindo em uma tabela:

Passo 2

Agora, pegando o nó D :

∑ F x = 0

4 5 5 4 P - F C D = 0

F C D = P

A energia de deformação será:

U = ∑ F 2 L 2 E A = 1 2 E A ∑ F ² L

U = 27 16 P 2 l E A

Como o trabalho da força é igual a:

P = 1 2 P ∆ = U

Logo:

∆ = 2 U P = 27 8   P l E A

∆ = 3,38 P l E A

Prontinho!

Resposta

∆ = 3,38 P l E A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usando o método do trabalho e energia, determinar a deflexão em C , provocada pela carga P .
Usando o método do trabalho e energia, determinar a deflexão em C , provocada pela carga P .
Usando o método do trabalho e energia, determinar a declividade no ponto D , devida ao momento M 0 .
Usando o método do trabalho e energia, determinar a declividade no ponto D , provocada pelo momento M 0 .
Usando o método do trabalho e energia, determinar a declividade no ponto D , devida ao momento M 0 .