Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 8.Problemas Revisão - Ex. 147

Para a viga com o carregamento mostrado, determinar a intensidade e a localização da maior deflexão do vão AB. Usar .

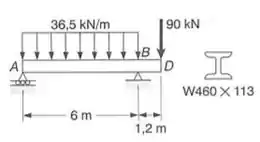
Passo 1

Para essa questão, por ser uma questão de revisão, podemos usar qualquer método que aprendemos, nesse caso, vou usar as nossas equações singulares, mas antes de de fato determinarmos as equações, vamos determinar as reações de apoio já que se trata de uma viga isostática, assim, teremos que:

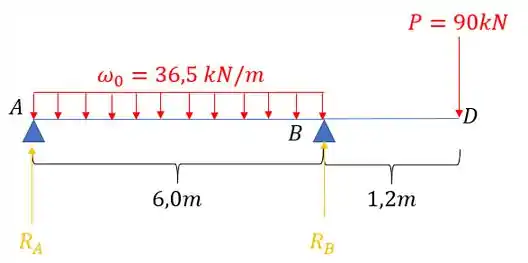
Separando por regiões temos:

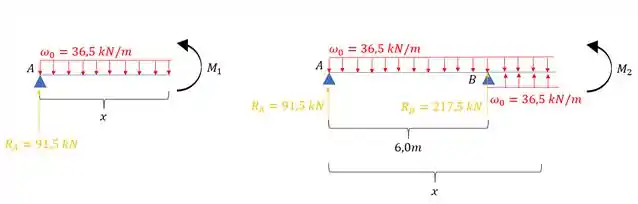
Assim temos que os momentos vão ser dados por:

E assim podemos definir o nosso momento fletor como sendo:

E esse momento que iremos usar na nossa equação, então vamos porá o próximo passo.

Passo 2

Sabemos que a equação que iremos relacionar a integração é dada por:

Integrando duas vezes teremos que:

E sabemos que as condições de contorno vão ser dadas por:

E assim podemos descobrir as nossas incógnitas.

Passo 3

Olhando cada uma das condições de contorno, vamos ter que:

Para o ponto inicial, consideramos as equações singulares iguais a zero por elas não estarem no intervalo que estamos, assim, podemos determinar que:

Aqui usamos a equação inteira, assim vamos ter que:

Assim a equação da deformação é dada por:

Como queremos a deformação entre A e B, podemos desconsiderar o trecho com as equações singulares, que fazem parte da segunda metade da viga, assim, temos que:

Como queremos a posição que ocorre a deformação máxima, basta derivarmos e igualarmos a nossa derivada a zero, assim, temos que:

Resolvendo na nossa equação temos que:

Como estamos falando de comprimentos, não podemos considerar valores negativos, e como estamos olhando o trecho AB, não consideramos valores acima de , assim, temos que: