Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 9.Problemas - Ex. 31
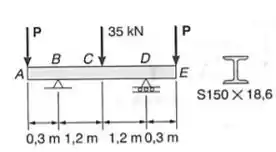
Para a viga com o carregamento mostrado, determinar:
- O valor de P para que a deflexão seja zero na extremidade A da viga;
- A variação dos valores de , para que o valor absoluto da deflexão na extremidade A da viga seja igual ou menor que .
Passo 1
E ai galera, até agora resolvemos apenas problemas com engastes, mas agora iremos começar a resolver problemas biapoiados, os conceitos vão se manter iguais aos que já conhecíamos, mas agora vamos ter que tomar um cuidado importante com o nosso diagrama de momentos fletores, então é de suma importância que fiquemos atento a ele, e por isso, vamos começar por ele, calculando primeiro a reação de apoio da nossa viga, teremos que:
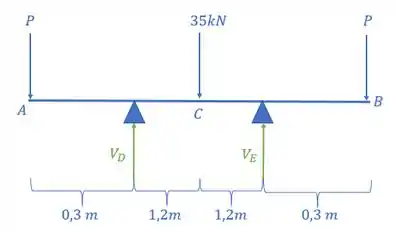
E por fim tem uma coisa bem legal de se notar, a nossa viga é simétrica com cargas simétricas, certo? Então não precisamos desenhar o diagrama inteiro da viga, podemos desenhar só metade do nosso diagrama, e analisando o que temos até aqui, vamos ver que é exatamente isso aqui:
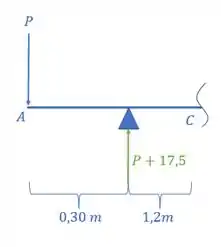
Assim o nosso diagrama de momentos fletores calculando um diagrama para cada carregamento será dado por:
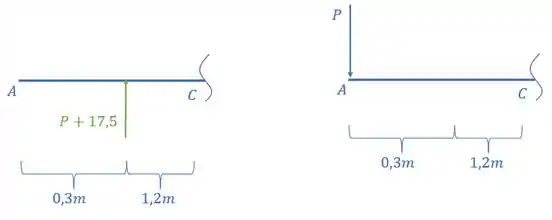
Porém, nesse caos em balanço iremos desconsiderar o carregamento em balanço na viga que só tem a reação de apoio, com isso, precisamso fazer , assim a nossa viga com seus respectivos diagramas, será dada por:
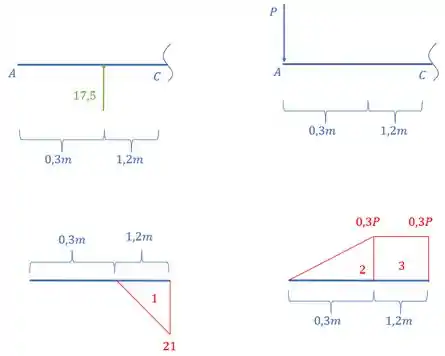
E por fim, temos que dividir o nosso diagrama pelo nosso , assim, teremos que:
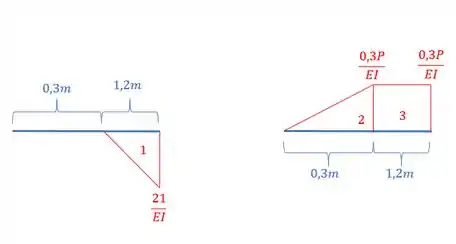
Passo 2
Agora precisamos determinar a deformação em dois pontos, um sendo a deformação no centro da nossa viga, e essa deformação já conhecemos a maneira de calcular ela, basta pegarmos as áreas entre o apoio e o centro e multiplicarmos a distância do centroide de cada área até o apoio, respeitando, é claro, os sinais que vimos no passo anterior, ou seja, estamos fazendo a deformação de B com relação a C, certo? Então podemos definir . Dessa maneira, teremos que:
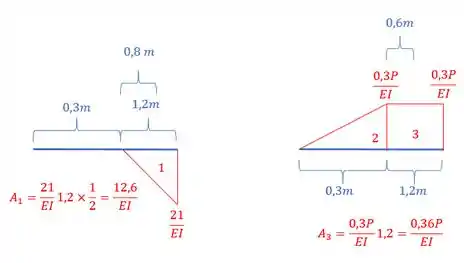
Perceba que somente as áreas 1 e 3 contribuem, dessa maneira, teremos que:
Como B é o apoio, temos que:
Vamos guardar essa equação por enquanto, porque lembre que nosso objetivo é determinar a deformação em A e não em C, e como calcular ela? O principio é muito parecido, porém aqui temos que a deformação é zero no ponto B e a de A é o que precisamos descobrir, porém, usaremos um novo conceito que é o seguinte:
E olha que interessante, o que estamos definindo aqui é que a deformação relativa total entre o ponto A que sobe e o ponto C que desce, é igual o total que A deforma menos o que C deforma com relação ao apoio, certo? E faz todo sentido, já que a deformação entre a extremidade e o meio soma as duas deformações, se eu souber quanto o meio deforma com relação ao apoio, eu consigo achar quanto a extremidade também deforma, e assim tudo fica na mais perfeita tranquilidade, certo?
Beleza, mas como determinar ? Da mesma maneira que determinamos , mas ao invés de determinarmos o centroide com relação ao apoio, determinaremos com relação a extremidade, e assim usaremos as 3 áreas e teremos que:
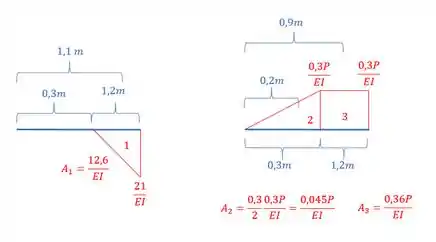
E temos que lembrar que:
Para o item A) queremos o valor de P para que o nosso ponto A não deforme, assim, temos que:
Para o item B) queremos que a deformação seja limitada no máximo a , assim temos que:
Pelo enunciado temos que:
E o momento de inércia da viga é dado por:
Assim teremos que:
Substituindo, teremos que: