Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 12.Problemas - Ex. 23

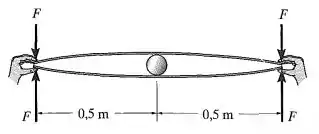
As partes centrais das duas fitas métricas de madeira estão separadas por um cilindro rígido liso de 50   m m de diâmetro. Determine a força F que deve ser aplicada a cada extremidade de modo que suas extremidades apenas se toquem. Cada fita tem 20   m m de largura e 5   m m de espessura. E m   =   11   G P a .

Passo 1

Para 0 ≤ x 1 ≤ 0,5   m :

∑ M = 0 M x 1 - F x 1   = 0 M x 1 = F x 1

Sabemos que:

E I d 2 v 1 d x 1 ² = M x

Logo:

E I d 2 v 1 d x 1 2 = F x 1

E I d v 1 d x 1 = F 2 x 1 2 +   C 1

E I v 1 = F 6 x 1 3 + C 1 x 1 + C 2

Passo 2

As condições de contorno serão:

x 1 = 0 → v 1 = 0

x 2 = 0 → v 2 = 0

Já as condições de continuidade serão:

x 1 = x 2 = 0,5 m → v 1 = v 2   e     d v 1 d x 1 = - d v 2 d x 2

Logo, substituindo:

C 1 = - 0,125 F ; C 2 = 0 ; C 3 = - 125 F ; C 4 = 0

Passo 3

Agora, temos que substituir na Equação da linha elástica. Fica assim:

v 1 = F 6 E I x 1 3 - 0,75 x 1 0,025 = F 6 × 11 × 10 9 × 0,02 × 0,005 3 12 0,5 3 - 0,75 × 0,5 F = 1,375   N

Resposta

F = 1,375   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a inclinação em B e o deslocamento em C. Os mancais em A e B exercem somente reações verticais sobre o eixo. EI é constante.
É possível que as vigas de plástico reforçado substituam as vigas de aço, pois seu peso é 1 4 destas. Utilizando a tabela do apêndice B, com σ a d m = 160 M P a e τ a d m = 84 M P a , selecione a viga
A viga está sujeita à carga mostrada na figura. Determine a inclinação em B e a deflexão em C. EI é constante.
A que distância a os mancais de apoio A e B devem ser colocados de modo que a deflexão no centro do eixo seja igual à deflexão em suas extremidades? Os mancais exercem somente reações verticais sobre
As duas componentes da força agem sobre o pneu do automóvel como mostra a figura. O pneu está fixo ao eixo, que é suportado pelos mancais em A e B. Determine a deflexão máxima do eixo. Considere que o