Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 14
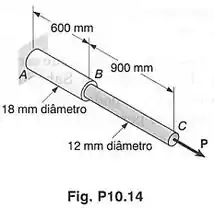
A barra é feita de uma liga de alumínio para a qual a tensão de escoamento é e o módulo de elasticidade é ; a barra é feita de um tipo de aço para o qual a e . Determinar a máxima energia de deformação que pode ser acumulada pela barra composta sem causar qualquer deformação permanente.
Passo 1
Oi, pessoa! Tudo tranquilinho? Animadão pra mais um exercício de energia de deformação?
A questão quer saber qual é a energia de deformação máxima que a barra pode absorver sem escoar. Essa barra é formada por duas partes diferentes: a parte 1 mais grossa feita de alumínio com módulo de elasticidade e tensão de escoamento e a parte 2 mais fina feita de aço com e .
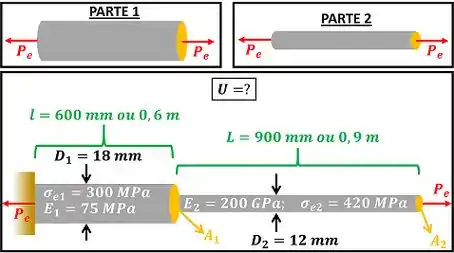
é a força que faz a barra começar a se deformar de forma permanente. Ou seja, é a força que gera uma tensão máxima na barra, fazendo a barra escoar. Em outras palavras, é a força máxima que faz a barra absorver a energia máxima ! Para achar o , temos que comparar a força que faz a parte grossa escoar com a força que faz a parte fina escoar. A menor das duas será a força que faz a barra total escoar!
é a área da seção transversal da parte mais grossa da barra . é a área da seção transversal da parte mais fina da barra .
Além disso, é o comprimento da parte mais grossa e é o comprimento da parte mais fina.
Tá, mas como podemos calcular a partir de ?
A barra é formada por duas partes com área constante: a parte 1 com área e a parte dois com área . Logo, sua energia de deformação máxima é a soma entra as energias de deformação da barra 1 e da barra 2 .
Como essas duas barras têm áreas de seção transversal constantes, podemos usar a fórmula 10.14 do livro que calcula as energias de deformação e delas.
Substituindo e na equação de :
Agora que temos todas essas informações em mãos, vamos calcular a força máxima aplicada sobre a barra no próximo passo!
Passo 2
Nesse passo nós vamos calcular quanto vale para depois calcular a energia de deformação da barra completa. Para isso, precisamos achar as áreas e em .
Antes de achar e , precisamos lembrar que a tensão vale e que a tensão vale .
Como é menor que , é igual a ! Logo:
Com esse valor em mãos, podemos achar no próximo passo.
Passo 3
Nesse passo, já podemos calcular . No entanto, antes de calcular , temos que lembrar que vale e que vale .
Substituindo esses valores na equação de :