Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 12.Problemas - Ex. 10

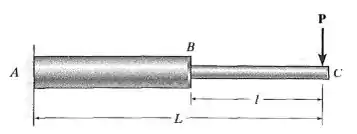
A viga é composta por duas hastes e está sujeita à carga concentrada P. Determine a inclinação em C. Os momentos de inércia das hastes são IAB e IBC e o módulo de elasticidade é E.

Passo 1

Faaaaala aí! O que ele quer aqui é que a gente ache a inclinação na ponta da viga. Mas repara que nós temos uma fica compostas por seções de momentos de inércia diferentes. Isso é importante.

Vamos continuar a usar que

E I d 2 v d x 2 = M x

Aí a gente acha o momento, integra uma veze (porque a gente só quer a inclinação) e acha θ x para esses dois casos.

E outro ponto de atenção: mesmo querendo o valor da inclinação em um ponto, precisamos analisar a inclinação nos dos intervalos, para que a gente consiga achar as constantes de integração.

Agora sim. Bora!

Passo 2

Antes de tudo, a gente só precisa especificar as reações dessa viga. Dá para fazer pelas equações de equilíbrio, ou no olho mesmo. O fato das seções serem diferentes não influencia essas equações. Fica assim:

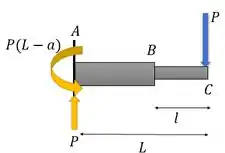
Bora achar o momentos para cada intervalo:

Para 0 ≤ x 1 ≤ l (origem do eixo x 1 em C )

M x 1 = - P x 1

Sabemos que:

E I d 2 v 1 d x 1 ² = M x

Logo:

E I d 2 v 1 d x 1 2 = - P x 1

E I d v 1 d x 1 = - P 2 x 1 2 +   C 1

E I θ 1 = - P 2 x 1 2 +   C 1

E aí a gente lembra que nesse intervalo I = I B C

E I B C θ 1 = - P 2 x 1 2 +   C 1

Passo 3

Para l ≤ x 2 ≤ L   (origem do eixo x 2 em C ).

M x 2 = - P x 2

Logo:

E I d 2 v 2 d x 2 2 = - P x 2

E I θ 2 = - P x 2 2 2 + C 3

E aí a gente lembra que nesse intervalo I = I A B

E I A B θ 2 = - P 2 x 2 2 +   C 3

Passo 4

Agora, vamos aplicar as condições de contorno. Nelas a gente retrata que a inclinação no apoio é nula. E há continuidade de θ onde as seções diferentes se encontram.

x 2 = L → θ 1 = d v 2 d x 2 = 0

B →     d v 1 d x 1 = d v 2 d x 2

Logo, substituindo nas nossas expressões

E I A B θ 2 = - P 2 x 2 2 +   C 3 → 0 = - P 2 L 2 + C 3 ∴ C 3 = P L 2 2

Para B :

x 1 = x 2 = l

E I B C θ 1 = - P 2 x 1 2 +   C 1

θ 1 = θ 2 → 1 I B C - P 2 x 1 2 +   C 1 = 1 I A B - P 2 x 2 2 +   C 3 →

→ 1 I B C - P 2 l 2 +   C 1 = 1 I A B - P 2 l 2 +   P L 2 2

C 1 = I B C I A B - P l 2 2 + P L 2 2 + P l 2 2

Passo 5

Aí a gente usa θ 1 , para achar a inclinação em C , ou seja, em x 1 = 0 :

E I B C θ 1 = - P 2 x 1 2 +   C 1

E I B C θ 1 = - P 2 x 1 2 +   I B C I A B - P l 2 2 + P L 2 2 + P l 2 2

θ c = - P 2 E 1 I A B L 2 - l 2 + l 2 I B C

Resposta

θ c = - P 2 E 1 I A B L 2 - l 2 + l 2 I B C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usando o método da Seção 5.2 , resolva o Problema 5 . 16 .Para a viga e o carregamento mostrados, determine a tensão normal máxima provocada pelo momento fletor na seção transversal C .
Trace os diagramas de força cortante e momento fletor para a viga e carregamento mostrados e, determine a tensão normal máxima provocada pelo momento fletor.
Para a viga e o carregamento mostrados na figura, projete a seção transversal da viga sabendo que o tipo da madeira utilizada tem uma tensão normal admissível de 1750p s i .
Para a viga e o carregamento mostrados na figura, projete a seção transversal da viga sabendo que o tipo da madeira utilizada tem uma tensão normal admissível de 1750p s i .
Para a viga e o carregamento mostrados na figura, projete a seção transversal da viga sabendo que o tipo da madeira utilizada tem uma tensão normal admissível de 12M P a .