Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 2.Problemas - Ex. 9

Parte de uma ligação de controle para um avião consiste em um membro rígido C B D e um cabo flexível A B . Se uma força é aplicada à extremidade D do membro e causa uma deformação normal no cabo de 0,0035   m m   /   m m , determine o deslocamento do ponto D . Originalmente, o cabo não é esticado.

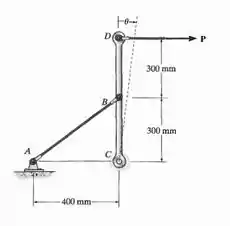
Passo 1

Fala aí galerinha, beleza? Partiu tirar 10 em Resmat. Vamos começar olhando a geometria desse problema. Segura na minha mão e vem!

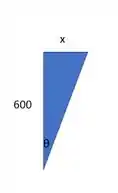
Antes da deformação, tínhamos algo assim:

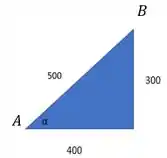
Onde o ângulo α   pode ser determinado por:

t g α = 300 400

α = 36,86 °

Note que a hipotenusa foi colocada direto por ser um triângulo conhecido, na dúvida, pode fazer Pitágoras.

Passo 2

Após a deformação, teremos:

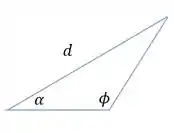
Onde ∅ = 90 + θ , pois é o ângulo de 90° do triângulo retângulo inicial mais o deslocamento de θ   causado pelo deslocamento de D .   Além disso, o lado d será os 500 m m   mais o alongamento (variação de comprimento) sofrido pela corda A B .

A deformação em A B   é:

ϵ = ∆ L L 0

Logo, o alongamento em A B   é:

∆ L = ε × L 0

∆ L = 0,0035 × 500 = 1,75

Logo, o comprimento d será:

d = 1,75 + 500 = 501,75 m m

Passo 3

Agora, temos a seguinte situação:

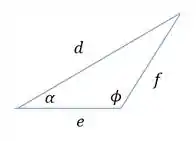
Pela lei dos cossenos, podemos determinar o ângulo ∅ :

d = f 2 + e 2 - 2 e f c o s ∅

Isolando o ∅ :

∅ = arccos ⁡ f 2 + e 2 - d 2 2 e f

Como o ângulo θ   é muito pequeno, podemos considerar o lado f   como inalterado, ou seja, como os 300 m m   iniciais . Substituindo:

∅ = arccos ⁡ - 0,00730

∅ = 90,41 °

Passo 4

Agora, como temos que:

∅ = 90 + θ = 90,41

Portanto:

θ = 0,41 °

Logo, temos a seguinte situação:

Onde x   é o deslocamento que queremos. Aplicando a tangente:

t g θ = x 600

t g 0,41 × 600 = x

x = 4,29 m m

Resposta

x = 4,29 m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um elemento estrutural de um reator nuclear é feito de uma liga de zircônio. Se esse elemento tiver se suportar uma carga axial de 20k N , determine a área da seção transversal exigida. Use um fator d
O poste é sustentado por um pino em C e por um arame de ancoragem AB de aço A - 36 . Se o diâmetro do arame for 5m m , determine quanto ele se deforma quando uma força horizontal de 15k N agir sobre o
A mudança de peso de um avião é determinada pela leitura de um extensômetro A montado no suporte de alumínio da roda do avião. Antes de o avião ser carregado, a leitura do extensômetro no suporte é ε
Os cabos de aço A B e A C sustentam a massa de 200k g . Se a tensão axial admissível para os cabos for σ a d m = 130 M P a , determine o diâmetro exigido para cada cabo. Além disso, qual é o novo comp
A viga é sustentada por um pino em C e por um cabo de ancoragem A B de aço A - 36 . Se o cabo tiver diâmetro de 5m m , determine quanto ele estica quando um carregamento distribuído w = 1,5k N / m agi