Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 67

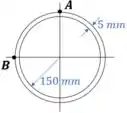
O tubo está sujeito a uma força de cisalhamento V = 40   k N . Determine o fluxo de cisalhamento no tubo nos pontos A e B

Passo 1

Dados da questão: V = 40   k N ,   r = 155 m m ,   r ' = 150 m m

A questão pede o fluxo de cisalhamento nos pontos A e B

Estratégia de resolução: A seção é simétrica por isso seu centroide é no meio, então vamos calcular o momento de inércia, depois o momento estático nos pontos de interesse e terminamos aplicando a equação de fluxo de cisalhamento em cada ponto.

Perceba que o ponto A está na extremidade superior, e por isso o cisalhamento neste ponto é zero, logo seu fluxo de cisalhamento também é zero: q A = 0

Passo 2

Momento de inércia:

I = π ⋅ 155 4 4 - π ⋅ 15 0 4 4

I = 55 , 72 ⋅ 10 6   m m 4

Passo 3

O momento estático em B é:

Podemos calcular esse momento de inércia subtraindo a seção amarela da seção verde:

Para um quadrante de circunferência temos:

A = 1 4 π r 2

y c = 4 r 3 π

Então o momento estático será:

Q = π ⋅ r 2 4 ⋅ 4 ⋅ r 3 π - π ⋅ r ' 2 4 ⋅ 4 ⋅ r ' 3 π

Q = 1 3 ( r 3 - r ' 3 )

Q = 116291 , 66 m m 3

Passo 4

Agora, só calcular o fluxo de cisalhamento em B:

q B = V Q I

q B = 40   k N ⋅ 116291 , 66   m m 3 55 , 72 ⋅ 10 6   m m 4

q B = 0,08327 k N m m

q B = 83,27 k N m

Resposta

q A = 0

q B = 83,27 k N m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o membro e carregamento do Prob. 5.72, determinar as tensões, normal e de cisalhamento, no ponto K .
Duas forças são aplicadas ao componente de máquinas A B D , como mostrado. Sabendo-se que a seção transversal do componente é retangular com 30x45m m , determinar as tensões, normal e de cisalhamento,
Várias pranchas são coladas juntas para formar a caixa mostrada. Sabendo-se que a viga é submetida a uma força cortante vertical de 3kN, determine a tensão de cisalhamento média na junta colada: (a) e
A viga composta é feita pela soldagem de perfis de aço laminado C200x17,1, as abas de um perfil de aço laminado W250x80, como mostrado. Sabendo-se que a viga é submetida a uma força cortante vertical
Várias pranchas são coladas juntas para formar a caixa mostrada. Sabendo-se que a viga é submetida a uma força cortante vertical de 3kN, determine a tensão de cisalhamento média na junta colada: (b) e