Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 120

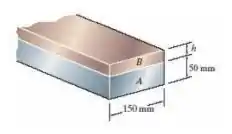
A viga composta é feita de alumínio 6061-T6 (A) e latão vermelho C83400 (B). Se a altura h = 40 mm, determine o momento máximo que pode ser aplicado à viga se a tensão de flexão admissível para o alumínio for (σadm)al = 128 MPa e para o latão (σadm)lat = 35 MPa.

Passo 1

Faaaala, meu povo bonito!! Tudo bem com vocês??

A nossa questão de hoje nos traz coisas um tanto quanto estranhas ali no meio, mas vou te explicar direitinho.

Saca só, o enunciado nos diz que a viga é composta de dois materiais, o alumínio (A) e o latão vermelho (B). Sabendo que a altura é h = 40   mm , o enunciado nos pede para determinar o momento máximo que pode ser aplicado à viga se a tensão de flexão admissível para o alumínio for:

σ a d m a l = 128   M P a

E para o latão vermelho:

σ a d m l a t = 35   M P a

A malandragem aqui, é que podemos calcular o momento máximo de cada material (alumínio e latão) separadamente!! O menor momento entre os dois vai ser o momento máximo da viga composta!! Afinal se o momento de máximo de algum dos dois materiais for ultrapassado, a viga vai se romper no lado desse material.

Belezoca, então vamos lá resolver rapidinho. Vem comigo!!

Passo 2

A primeira coisa que precisamos achar é a relação entre os coeficientes E a l e E l a t . Como E a l = 68,9 e E l a t = 101 , obtemos que:

n = 68,9 101

n = 0,682

Além disso, o enunciado nos deu que o comprimento da viga é 150   mm , sendo assim:

b ' = n b

b ' = 0,682 × 150

b ' = 102,327   mm

Agora podemos determinar o centroide da seção transversal, dado como:

y C G = ∑ A y C G ∑ A

y C G = 102,327 50 25 + 150 40 70 102,327 50 + 150 40  

Portanto:

y C G = 49,289   mm

Passo 3

Show de bolinhas, agora só falta a gente encontrar o momento de inércia da viga pra substituir tudo na fórmula da tensão, então bora lá!

O momento de inércia será dado como:

I = 0,102327 × 0,05 3 12 + 0,102327 × 0,05 × 0,024289 2 + 0,15   x   0,04 3 12 + 0,15 × 0,0413 × 0,02071 2

I = 7,45799 × 10 - 6   m 4

Belezoca, agora temos todos os elementos da fórmula da tensão máxima:

σ m á x = M m á x y C G I

Mas como queremos determinar o momento máximo, vamos isolar ele:

M m á x = I σ m á x y C G

Então para o alumínio, o enunciado nos deu que σ a d m a l = 128   M p a , sendo assim:

M m á x a l = I σ a d m a l y C G

Logo:

M m á x a l = 7,45799 × 10 - 6   128 49,289

M m á x a l = 28,4   kN.m

Enquanto que para o latão vermelho, temos que σ a d m l a t = 35   M P a , segue que o momento máximo será:

M m á x l a t = 7,45799 × 10 - 6   35 49,289

M m á x l a t = 6,41   kN.m

Portanto, como o momento do latão, M m á x l a t = 6,41   kN.m , é menor que o momento do alumínio, M m á x a l = 28,4   kN.m , quer dizer que o momento máximo da viga será:

M m á x = 6,41   kN.m

Resposta

M m á x = 6,41   kN.m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma placa de aço, com 160m m de largura e 8m m de espessura, é dobrada para formar a viga em forma de U mostrada na figura . Sabendo que a força vertical P atua em um ponto do plano médio da alma do U
Para a barra composta indicada, determine o maior momento fletor admissível quando a barra é flexionada em torno do eixo vertical. Barra do problema 4.33 .
Uma barra com a seção transversal mostrada na figura foi construída unindo-se firmemente latão e alumínio. Usando os dados fornecidos abaixo, determine o maior momento fletor admissível quando a barra
Vigas de madeira e chapas de aço são aparafusadas firmemente para formar o elemento composto mostrado na figura. Usando os dados da tabela abaixo, determine o maior momento fletor admissível quando a
Uma barra com a seção transversal mostrada na figura foi construída unindo-se firmemente latão e alumínio. Usando os dados fornecidos abaixo, determine o maior momento fletor admissível quando a barra