Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 13.Problemas - Ex. 13
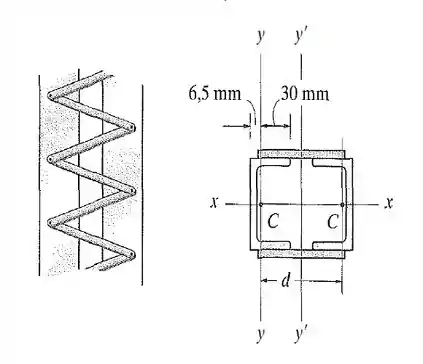
13. Os dois perfis em U de aço devem ser interligados para formar uma coluna da ponte de de comprimento que consideramos estar acoplada por pinos nas extremidades. Cada perfil em tem área de seção transversal e momentos de inércia , . A figura mostra a localização do centroide C de sua área. Determine a distância adequada entre os centroides dos perfis em , de modo que ocorra flambagem em torno dos eixos e devido à mesma carga. Qual é o valor dessa carga crítica? Despreze o efeito da interligação. ,
Passo 1
Bem! Vamos entender esse enunciado grandão! O que ele quer dizer é que a gente tem uma coluna, e seção dessa coluna é a junção de dois perfis U.
Então na verdade, vamos usar todos os nossos conhecimentos de flambagem de colunas aqui, levando em consideração que nossa seção é formada por esses dois U’s posionados a uma distância , que queremos descobrir, ok?
Essa distância permite que a nossa coluna sofra flambagem em torno dos dois eixos por causa de uma mesma carga crítica.
Como as extremidades estão presas por pinos, de cara já tiramos que o fator de comprimento efetivo , é igual a .
Outros dados:
E para um perfil U sozinho, temos que:
Bora começar!
Passo 2
Vamos tratar de obter o momentos de inércia em relação ao eixo da nossa seção completa.
Como o enuciado diz claramente que há dois perfis e nos informa os momentos de inércia em relação a e desses perfis; para encontrar o momento resultante em basta multiplicar por dois o que nos é fornecido.
Agora para encontrar o momento em , se observar na figura do enunciado, vamos ver que teremos que usar o teorema dos eixos paralelos.
Passo 3
Só que a questão nos pede a distância adequada entre os centroides dos perfis em , de modo que ocorra flambagem em torno dos eixos e devido à mesma carga. Olha a fórmula da carga crítica para flambagem:
Para os dois eixos, esses valores são iguais, exceto os momentos de inércia. A carga crítica para cada eixo seria:
Se a gente quer que elas sejam iguais, podemos fazer:
Ora bolas! A distância adequada vai ser quando o momento de inércia em for igual ao momento de inércia em :
Esse valor é maior do que , da figura do enunciado, o valor mínimo a partir do qual a gente pode montar a coluna com essa seção. Então, tudo ok por aqui.
Passo 4
Vamos então, usar a fórmula da carga crítica para a flambagem:
E substituindo os valores numéricos pertencentes a cada variável, chegamos até: