Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 25

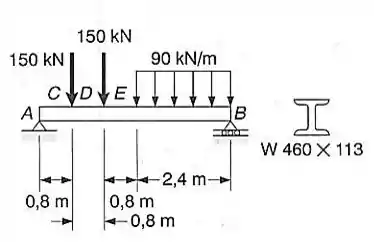
Para a viga e o carregamento mostrado, determinar: a) máxima tensão normal numa seção transversal em D; b) a máxima tensão de cisalhamento numa transversal imediatamente à direita de A. Assumir que τ= V/A(alma)

Passo 1

E ai gurizada tudo beleza? Espero que sim!!

Vamos calcular o somatório do momento para achar, o VB pode ser? Vem comigo!!! Lembrando que a setinha para baixo consideramos o valor como negativo!

Mas antes lembrem-se que devemos tornar a carga distribuída em pontual = =   90   × 2,4

= 216   K N

Agora sim podemos encontrar VB, venha cmg :D

M =   F   × d

Σ M A = - 1 50 × 0 , 8 - 1 50 × 1 , 6 - 216 × 3 , 6 + V B × 4,8 = 0

V B = - 237   K N

Agora gurizadaa vamos realizar o somatório das forças na vertical para achar VA

Σ F y = V A - 1 50 - 150 - 216 + 237 = 0

V A = 2 79   K N

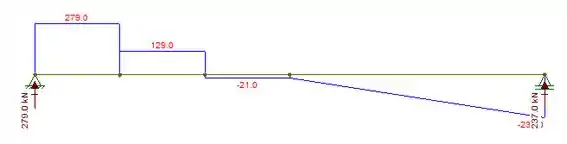
Agora podemos desenhar o diagrama de força cortante ;)

Passo 2

  1. Agora vamos determinar a força cortante? Vem comigo!!!

    2. Para realizarmos esse diagrama pensem comigo, eu falei para vocês antes que a seta para baixo é negativo certo? Lembrando da esquerda para a direita

    Então no 1º quadrante fica temos: V A = 2 79   K N

    2º quadrante: 2 79 - 150 =   12 9   K N

    3º quadrante: 12 9 - 1 50 = - 21 K N

    4º quadrante: V B = - 237   K N

    Agora vamos calcular comigo o momento fletor, 3 reações= 3 momentos, basta multiplicarmos a força pela distância expressa no diagrama, para todos os pontos.

    Σ M = 2 79   × 0,8 = 223,2   K N m

    Σ M = 279   × 1 , 6 - 15 0 × 0,8 = 326,4   K N m

    Σ M = - 216   × 1 , 2 + 237 × 2,4 = 309,6   K N m

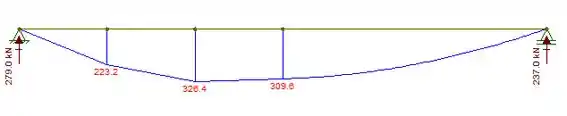
    Agora podemos encontrar a tensão normal

    Primeiramente temos que calcular a área do perfil em “I” abaixo, para isso vamos considerar como se fosse um quadrado para facilitar o cálculo beleza?

    A = 2 × 280   × 17,3 + 428,4 × 10,8 = 14314,72   m m ²

    Agora podemos achar a Inercia (Iz) ..

    I z = B × h 3 / 12

    I z 1 = 280 × 463 3 12 = 2315899763   m m ²

    Galera como consideramos acima um quadrado, e temos perfil em I, temos que descontar as áreas vazadas, considerando como se fossem dois quadrados e depois calcular a inércia usando a mesma fórmula acima.

    I z 2 = 881885496,6   m m 4

    Agora: I Z = I z 1 - I z 2 = 2315899763   m m 4 - 881885496,6   m m 4 = 552128769,7   m m 4

    Agora sim podemos achar a tensão

    σ = m × Y I z

    σ = 326,4 × 10 6 × 231,5 552128769,7 = 136,85   M P a

    Passo 3

  2. Máxima tensão de cisalhamento

σ = V × Q I z × t = V × A × y I z × t

σ = 2 7900 × ( 280 × 17,3 ) × ( 231,5 - 17,3 2 ) 4608000 × 10,8 = 62,1   M P a

Resposta

  1. σ = 136,85   M P a
  2. σ = 62,1     M P a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um tubo de aço de 400 mm de diâmetro externo é fabricado a partir de uma chapa de aço com 10 mm de espessura, soldada ao longo de uma hélice que forma um ângulo de 20° com um plano perpendicular ao ei
O vínculo BC com 6 mm de espessura, e é feito de aço com uma resistência máxima à tração de 450 MPa. Qual deve ser sua largura w se a estrutura mostrada estiver sendo projetada para suportar uma carga
Os elementos AB e BC da treliça mostrada são feitos da mesma liga. Sabe-se que uma barra quadrada de 20 mm de lado feita do mesmo material foi ensaiada até falha e que uma carga final de 120 kN foi re
Os elementos AB e BC da treliça mostrada são feitos da mesma liga. Sabe-se que uma barra quadrada de 20 mm de lado feita do mesmo material foi ensaiada até falha e que uma carga final de 120 kN foi re
O vínculo AB deve ser feito de aço para o qual a tensão normal é de 450 MPa. Determine a área da seção transversal da AB para a qual o fator de segurança será 3,50. Suponha que o vínculo seja reforçad