Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 31

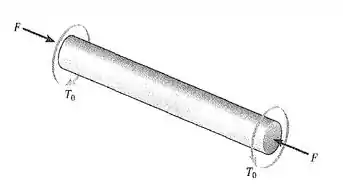
31. O eixo tem diâmetro d e está sujeito às cargas mostradas. Determine as tensões principais e a tensão de cisalhamento máxima no plano desenvolvida em qualquer lugar na superfície do eixo.

Passo 1

Aqui, vamos primeiro montar o diagrama de corpo livre da viga:

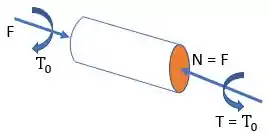
Passo 2

Agora, calcularemos a tensão no eixo:

σ = - F A

σ = - F π 4 d 2

Onde d é o diâmetro da nossa seção transversal. Ficamos então, com:

σ = - 4 F π d 2   ( U n i d a d e s   e m   P a s c a l )

E agora, bora fazer o cálculo da tensão máxima de cisalhamento no ponto A :

τ = T c J

Lembrando que o momento polar de inércia de um círculo é dado pela fórmula:

J = π 2 r 4

A tensão de cisalhamento, desse jeito, vai ter a seguinte cara:

τ = T 0 c π 2 c 4

Como c =   d / 2 :

τ = T 0 c π 2 d 2 4

τ = 16 T 0 π d 3 ( U n i d a d e s   e m   P a s c a l )

Passo 3

Calcularemos, então, as tensões principais do eixo:

σ 1,2 = σ x + σ y 2 ± σ x - σ y 2 2 + τ x y 2

σ 1,2 = - 4 F π d 2 - 0 2 ± - 4 F π d 2 - 0 2 2 + ( 16 T 0 π d 3 ) 2

σ 1,2 = - 2 F π d 2   M P a ± 2 π d 2 F 2 + 64 T 0 2 d 2   M P a

Com isso obtemos duas tensões, σ 1 e σ 2 :

σ 1 = - 2 F π d 2   M P a + 2 π d 2 F 2 + 64 T 0 2 d 2   M P a

σ 1 = 2 π d 2 - F + F 2 + 64 T 0 2 d 2 ( U n i d a d e s   e m   P a s c a l )

σ 2 = - 2 F π d 2   M P a - 2 π d 2 F 2 + 64 T 0 2 d 2   M P a

σ 2 = - 2 π d 2 F + F 2 + 64 T 0 2 d 2 ( U n i d a d e s   e m   P a s c a l )

Passo 4

Logo em seguida, vamos calcular a tensão de cisalhamento máxima no plano τ m á x , pela seguinte fórmula:

τ m á x = σ x - σ y 2 2 + τ x y 2

τ m á x = - 4 F π d 2 - 0   2 2 + 16 T 0 π d 3 2

τ m á x = - 2 F π d 2 2 + 16 T 0 π d 3 2

            τ m á x = 2 π d 2 F 2 + 64 T 0 2 d 2   ( U n i d a d e s   e m   P a s c a l )

Resposta

Tensões principais no eixo:

σ 1 = 2 π d 2 - F + F 2 + 64 T 0 2 d 2   ( U n i d a d e s   e m   P a s c a l )

σ 2 = - 2 π d 2 F + F 2 + 64 T 0 2 d 2   ( U n i d a d e s   e m   P a s c a l )

Tensão de cisalhamento máxima no eixo:

            τ m á x = 2 π d 2 F 2 + 64 T 0 2 d 2   ( U n i d a d e s   e m   P a s c a l )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

13. O estado de tensão em um ponto é mostrado no elemento. Determine:(a) as tensões principais e (b) a tensão de cisalhamento máxima no plano e a tensão normal média no ponto. Especifique a orientação
16. O estado de tensão em um ponto é mostrado no elemento. Determine:(a) as tensões principais e (b) a tensão de cisalhamento máxima no plano e a tensão normal média no ponto. Especifique a orientação
18. A barra de aço tem espessura de 12 mm e está sujeita à carga periférica mostrada na figura. Determine as tensões principais desenvolvidas na barra.
20. A tensão que age nos dois planos em um ponto é indicada na figura. Determine a tensão de cisalhamento no plano a - a e as tensões principais no ponto.
21. A tensão que age nos dois planos em um ponto é indicada na figura. Determine a tensão normal σ b e as tensões principais no ponto.