Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 6.Problemas - Ex. 25
Uma viga com a seção transversal mostrada é submetida a uma força cortante vertical . Determine (a) a linha horizontal ao longo da qual a tensão de cisalhamento máxima. (b) a constante k na expressão a seguir para a tensão de cisalhamento máxima.
em que é a área da seção transversal da viga
Passo 1
E ai gurizada, tudo beleza? O enunciado pede que a gente determine a linha horizontal ao longo da qual a tensão de cisalhamento máxima a constante k na expressão a seguir para a tensão de cisalhamento máxima. Considere o esboço abaixo :D
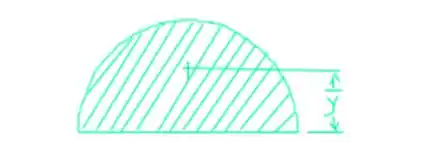
Passo 2
Considere as equações abaixo :D
e
Para o semicírculo, temos:
- ocorre no centro onde
Passo 3
Então para determinarmos a constante k na expressão a seguir para a tensão de cisalhamento máxima, temos:
Resposta
(a)
(b)
Exercícios de Livros Relacionados
Os mancais em A e D exercem somente as componentes y e z da força sobre o eixo. Se τ a d m = 60M P a , determine, com aproximação de 1m m , o eixo de menor diâmetro que suportará a carga. Use a teoria
Os mancais em A e D exercem somente as componentes y e z da força sobre o eixo. Se τ a d m = 60 MPa, determine, com aproximação de 1 mm, o eixo de menor diâmetro que suportará a carga. Use a teoria da
Os mancais em A e D exercem somente as componentes y e z da força sobre o eixo. Se τ a d m = 60M P a , determine, com aproximação de 1m m , o eixo de menor diâmetro que suportará a carga. Use a teoria
Resolva o Problema 11.38 usando a teoria de falha da energia de distorção máxima com σ m á x = 180M P a á .
As polias acopladas ao eixo estão carregadas como mostra a figura. Se os mancais em A e B exercerem somente forças horizontais e verticais sobre o eixo, determine, com aproximação de 1m m , o diâmetro