Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 53

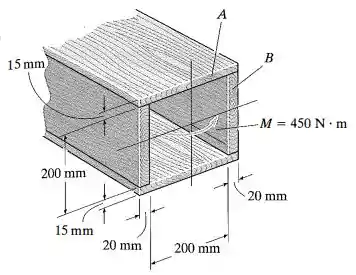
A viga é composta por quatro peças de madeira coladas como mostra a figura. Se o momento que age na seção transversal for M = 450   N · m , determine a força resultante que a tensão de flexão produz na peça superior A e na peça lateral   B .

Passo 1

Fala aí pessoal, vamos para mais um exercício de resmat. Primeiro, vamos determinar o DCL:

Passo 2

E então, calular o momento de inércia da seção. Para isso, vamos considerar que:

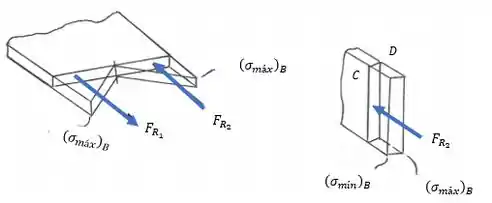
I = b h 3 12 - b ' h ' 3 12 I = 0 , 240 × 0,230 3 12 - 0 , 200 × 0,2 00 3 12 I = 1,316 × 10 - 4   m 4

Com isso, podemos calcular a resultante em A, temos:

F R A = 0,02 × 0,015 σ T m á x - 0,02 × 0,015 σ T m á x F R A = 0   k N

Passo 3

Em seguida, a tensão máxima em B é dada por:

σ B m á x = M c I = 450 × 0,120 1,316 × 10 - 4 σ B m á x = 410,33   k P a

E a tensão mínima em B é dada por:

σ B m í n = M c I = 450 × 0,1 00 1,316 × 10 - 4 σ B m í n = 341 , 87   k P a

Com isso, a força resultante em B vai ser de:

F R B = 410,33 + 341,87 0,02 × 0,2 2 F R A = 1,50   k N

Resposta

F R A = 0   k N

F R A = 1,50   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considerando que a reação do solo é uniformemente distribuída, trace os diagramas de força cortante e o momento fletor para a viga e carregamento mostrados, e determine o valor máximo absoluto ( a ) d
Para a viga e o carregamento mostrados, determine a tensão normal máxima provocada pelo momento fletor na seção transversal C .
Trace os diagramas de força cortante e momento fletor para a viga e carregamento mostrados na figura, e determine a tensão normal máxima gerada pelo momento fletor.
Trace os diagramas de força cortante e momento fletor para a viga e carregamento mostrados na figura, e determine a tensão normal máxima gerada pelo momento fletor.
Considerando que a reação do solo é uniformemente distribuída, trace os diagramas de força cortante e o momento fletor para a viga e carregamento mostrados, e determine o valor máximo absoluto ( a ) d