Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 36
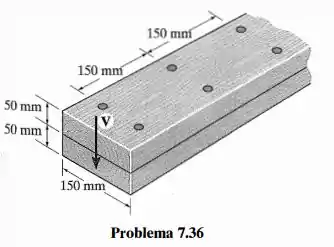
A viga é construída com duas tábuas presas uma à outra na parte superior e na parte inferior por duas fileiras de pregos espaçados de 150 mm. Se cada prego puder suportar uma força de cisalhamento de 2,5 kN, determine a força de cisalhamento máxima V que pode ser aplicada à viga.
Passo 1
A questão nos fornece os seguintes dados:
A questão pede o valor máximo para a força
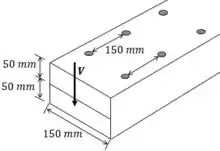
Estratégia de resolução:
De maneira geral, começamos a resolver as questões de fluxo de cisalhamento calculando as propriedades geométrica: Centroide, Momento de Inércia e Momento Estático.
Tenha atenção na hora de escolher a seção onde calcular o momento estático, é neste ponto em que ocorrem a maior quantidade de erros.
Por fim aplicamos a equação de fluxo de cisalhamento, e igualamos ela à capacidade do prego de resistir ao fluxo de cisalhamento.
Passo 2
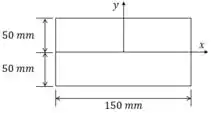
Começamos calculando o centroide: Por ser uma viga perfeitamente simétrica, o centroide fica no meio da seção transversal.
Vamos desenhar um sistema de eixos coordenados em cima do centroide. Isso irá facilitar o cálculo do momento de inércia:
Passo 3
Agora calculamos o momento de inércia de toda a seção transversal
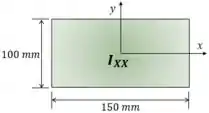
O momento de inércia de um retângulo é
Passo 4
Agora vamos escolher e calcular o momento estático.
Neste caso a escolha do momento estático é simples, como mostra região destacada abaixo, vamos simplesmente selecionar a tábua de cima (ou a de baixo, o resultado seria o mesmo):
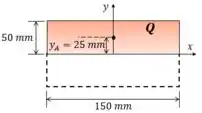
E agora calculamos o momento estático
Passo 5
Observe na figura abaixo:
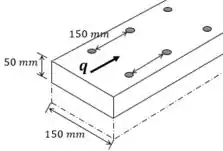
Observe que o à medida que o fluxo de cisalhamento avança ao longo da viga, ele é resistido por dois pregos. Assim, podemos definir o fluxo de cisalhamento como:
Por outro lado, a fórmula para o fluxo de cisalhamento é
Igualando as duas equações: