Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 47

A viga é fabricada com dois perfis em U equivalentes e duas chapas. Cada chapa tem altura de 150 mm e espessura de 12 mm. Se um cisalhamento V = 250   k N for aplicado à seção transversal, determine o espaçamento máximo entre os parafusos. Cada parafuso pode resistir a uma força de cisalhamento de 75   k N .

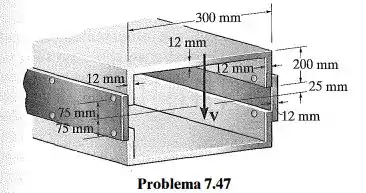
Passo 1

Dados da questão: V = 2 50   k N ,   F p a r a f u s o = 75   k N

A questão pede o espaçamento entre parafusos: s = ?

Primeiro calculamos o momento de inércia, depois calculamos o momento estático em uma das vigas em U. Esta viga em U está com parafuso em ambas as abas, e seu fluxo de cisalhamento será dividido entre dois parafusos. Com isso poderemos aplicar as equações de fluxo de cisalhamento para determinar o espaçamento.

OBS: A seção é simétrica, por isso seu centroide é centralizado

Passo 2

Pra calcular o momento de inércia vamos calular o retângulo cinza, somar com os dois retângulos cinza escuro e subtrair os retângulos amarelo e laranjas.

I U = 1 12 ⋅ 0,300 ⋅ 0.25 3 - 1 12 ⋅ 0.024 ⋅ 0.050 3 - 1 12 ⋅ 0.300 - 0.024 ⋅ 0.25 - 0.024 3

I U = 390.625 × 10 - 6 - 250 × 10 - 9 - 265.493 × 10 - 6

I U = 390.625 - 265.743

I U = 124.882 × 10 - 6

I P = 1 12 ⋅ 0.024 ⋅ 0.15 3

I P = 6.75 × 10 - 6 m 4

I = I U + I P

I = 131.632 × 10 - 6 m 4

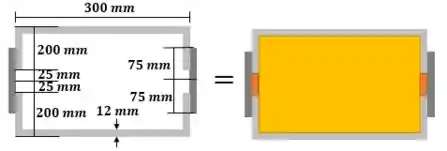
Passo 3

Calcularemos o momento estático da seção em U

Q = 0,300 ⋅ 0,012 ⋅ 0.5 ⋅ 0.25 - 0.5 ⋅ 0,012 +

+ 2 ⋅ 0,012 ⋅ 0,088 ⋅ ( 0.5 ⋅ 0,088 + 0.5 ⋅ 0,050 )

Q = 3.6 × 10 - 3 ⋅ 125 × 10 - 3 - 6 × 10 - 3 + ( 145.728 × 10 - 6 )

Q = 428.4 × 10 - 6 + ( 145.728 × 10 - 6 )

Q = 574.128 × 10 - 6   m 4

Passo 4

Na viga em U que selecionamos o cisalhamento é dividido em dois parafusos, então o fluxo de cisalhamento sobre o parafuso é:

q = 2 F p a r a f u s o s

E a fórmula do fluxo de cisalhamento é:

q = V Q I

Igualando as expressões:

2 F p a r a f u s o s = V Q I

Isolando o s :

s = 2 F p a r a f u s o I V Q

s = 2 ⋅ 131.632 × 10 - 6 ⋅ 75 × 10 3 250 × 10 3 ⋅ 574.128 × 10 - 6

s = 19.7448 143.532

s = 0.137563748   m

Resposta

s ≅ 137.564   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A escora está sujeita a um cisalhamento vertical V = 130 k N . Construa um gráfico da intensidade da distribuição de tensão de cisalhamento que age na área da seção transversal e calcule a força de ci
Determine a força de cisalhamento máxima V que a escora pode suportar se a tensão de cisalhamento admissível para o material for τ a d m = 40M P a
Faça um gráfico da intensidade da tensão de cisalhamento distribuída na seção transversal da escora se ela for submetida a uma força de cisalhamento V = 15 k N .
A viga é composta por três tábuas coladas nas linhas de junção A e B. Se for submetida ao carregamento mostrado na figura, determine a tensão de cisalhamento desenvolvida nas juntas coladas na seção a
A viga está sujeita a uma carga uniforme w. Determine a localização a dos apoios de modo que a tensão de cisalhamento na viga seja a menor possível. Qual é essa tensão?