Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 88

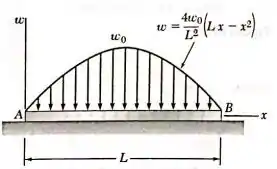
A viga A B , que esta disposta sobre o solo, sustenta a carga parabólica mostrada na figura. Considerando que a reação para cima do solo é uniformemente distribuída, a escreva as equações das curvas de esforço cortante e de momento fletor, b determine o máximo momento fletor.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Temos o seguinte diagrama de corpo livre:

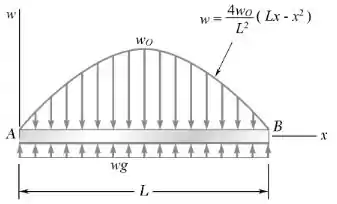
Suponha que a força na direção y positiva seja positiva:

↑ + ∑ F y = w R L - ∫ 0 L 4 w o L 2 L x - x 2 d x

Tomando a condição de equilíbrio, temos:

∑ F y = 0

w R L - ∫ 0 L 4 w o L 2 L x - x 2 d x = 0

Resolvendo, temos:

w R L - 4 w o L 2 L x 2 2 - x 3 3 0 L = 0

w R L - 4 w o L 2 L L 2 2 - L 3 3 - 0 + 0 = 0

w R L = 2 w o L 3

w R = 2 w o 3

Passo 2

Seja:

ξ = x L

Logo:

d ξ = d x L

d x = L d ξ

A função do carregamento será:

w x = 4 w o L 2 L x - x 2 - 2 w o 3

w x = 4 w o L 2 L ξ L - ξ L 2 - 2 w o 3

w x = 4 w o ξ - ξ 2 - 1 6

Passo 3

A equação da cortante é encontrada usando a seguinte derivada:

d V d x = - w x

V = ∫ 0 ξ 4 w o ξ - ξ 2 - 1 6 L d ξ

Resolvendo, temos:

V = - 4 w o L ξ 2 2 - ξ 3 3 - ξ 6 0 ξ

V = - 4 w o L ξ 2 2 - ξ 3 3 - ξ 6

Voltando para a coordenada x , temos:

V = - 4 w o L x L 2 2 - x L 3 3 - x L 6

V x = - w o x 2 x L - 4 x 2 3 L 2 - 2 3

Passo 4

Temos também que a derivada da função do momento fletor é igual a função da força cortante. Portanto:

d M d x = V x

M x = ∫ V x d x

Substituindo, temos que:

M x = ∫ 0 x - w o x 2 x L - 4 x 2 3 L 2 - 2 3 d x

Resolvendo, temos que:

M x = - w o 2 x 3 3 L - x 4 3 L 2 - x 2 3

Passo 5

Para a intensidade e a localização do máximo momento fletor, temos:

M m á x → V x = 0

V x = - w o x 2 x L - 4 x 2 3 L 2 - 2 3 = 0

Resolvendo, temos que:

x = L 2

Aplicando na equação do momento, teremos:

M m á x = - w o 2 L 2 3 3 L - L 2 4 3 L 2 - L 2 2 3

Resolvendo, encontramos:

M m á x = w o L 2 48

Resposta

a ) V x = - w o x 2 x L - 4 x 2 3 L 2 - 2 3

M x = - w o 2 x 3 3 L - x 4 3 L 2 - x 2 3

b )   M m á x = w o L 2 48

x = L 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine  a  força  em  cada  membro  da  treliça  e  indique  se  os  membros  estão  sob  tração  ou  compressão.
Determine a força em cada membro da treliça e  indique se os membros estão sob tração ou compressão. Considere P1 = 45 kN, P2 = 30 kN.
A treliça, usada para sustentar uma sacada, está sujeita às cargas mostradas. Considere cada nó como um pino e determine a força em cada membro. Indique se os membros estão sob tração ou compressão.
Determine a força em cada membro da treliça e indique se os membros estão sob tração ou compressão. Considere P = 8 kN.
Determine a força em cada membro da treliça em função da carga P e indique se os membros estão sob tração ou compressão.