Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 87

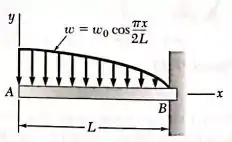
Para a viga e o carregamento mostrados nas figuras, a deduza as equações das curvas de esforço cortante e momento fletor, b determine a intensidade e a localização do máximo momento fletor.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

De acordo com o enunciado a equação da carga pode ser descrita por:

w x = w o cos ⁡ π x 2 L  

Sabemos que:

d V d x = - w ( x )

Logo:

V x = - ∫ w x d x

Passo 2

Nós temos V x = - ∫ w x d x . Substituindo, temos:

V x = - ∫ w o cos ⁡ π x 2 L   d x

V x = - w o 2 L π sen ⁡ π x 2 L + C 1

Passo 3

Temos também que a derivada da função do momento fletor é igual a função da força cortante. Portanto:

d M d x = V x

M x = ∫ V x d x

Substituindo, temos que:

M x = ∫ - w o 2 L π sen ⁡ π x 2 L + C 1 d x

Resolvendo, temos que:

M x = w o 2 L π 2 cos ⁡ π x 2 L + C 1 x + C 2

Passo 4

Para calcular as constantes, vamos substituir V x e M x no ponto x = 0 .

V 0 = - w o 2 L π sen ⁡ π 0 2 L + C 1

V 0 = C 1 = 0

Logo:

M 0 = w o 2 L π 2 cos ⁡ π 0 2 L + 0 0 + C 2

C 2 = - w o 2 L π 2

Portanto, as equações serão:

V x = - w o 2 L π sen ⁡ π x 2 L

E:

M x = w o 2 L π 2 cos ⁡ π x 2 L - w o 2 L π 2

M x =   w o 2 L π 2 cos ⁡ π x 2 L - 1

Passo 5

Para a intensidade e a localização do máximo momento fletor, temos:

M m á x → x = L

M m á x = w o 2 L π 2 cos ⁡ π L 2 L - 1

M m á x = w o 2 L π 2

Resposta

a ) V x = - w o 2 L π sen ⁡ π x 2 L

M x =   w o 2 L π 2 cos ⁡ π x 2 L - 1

b )   M m á x = w o 2 L π 2

x = L

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga simplesmente apoiada é feita de madeira com tensão de flexão admissível σ a d m =6,5 MPa e tensão de cisalhamento admissível τ a d m = 500k P a . Determine as dimensões da viga se ela tiver de
73- Usando o método da Seção 7.6 , resolva o Problema 7.41
70- Para a viga e o carregamento mostrados nas figuras, ( a ) trace os diagramas de esforço cortante e de momento fletor, ( b ) determine os valores absolutos máximos do esforço cortante e do momento
Determine a força em cada membro da treliça e  indique se os membros estão sob tração ou compressão. Considere  θ = 30 ° .
Determine a força em cada membro da treliça e indique se os membros estão sob tração ou compressão.